72
ein Gesamt-CLV von 1818,17 €
0
resultiert.
Wenn nun zu Recht eingeworfen wird, dass kein
Kunde unendlich lange leben wird, so gibt es
zwei Antworten. Zunächst kann darauf hinge-
wiesen werden, dass die späten Einzahlungs-
überschüsse aufgrund der hohen Abzinsung
und der fortgeschrittenen Kündigungen kaum
noch einen Effekt ausüben. Als zweites kann die
Kalkulation aber auch nach z. B. 10 Jahre been-
det werden, in dem der Terminal Value, der sich
ab Jahr 11 ergibt, wieder abgezogen wird.
Wenn er auf t=0 bezogen wird, beträgt er nur
46,22 €
0
, was nur eine geringe Reduktion des
Gesamt-CLV von 2,55% bedeutet.
Die beschriebene Berücksichtigung der Retenti-
on Rate über die Grundlaufzeit von 4 Jahren hi-
naus ist besonders dann wichtig, wenn die Kun-
dengruppe sich in den Retention Rates unter-
scheiden, wie es im Beispiel von Meffert/Bruhn/
Hadwich (S. 491) der Fall ist. Nach einer Reten-
tion Rate von 75% für die erste Kundengruppe
unterstellen sie 50% für die zweite Gruppe und
90% für die dritte. Es ist offensichtlich, dass die
zweite Kundenbasis bei einem jährlichen Verlust
von 50% stark schwindet, so dass der Fehler
des Abbruchs nach 4 Jahren nicht so schlimm
ist. Dies ist aber fatal für die dritte Kundengrup-
pe, die im Beispiel jedes Jahr nur um 10% ab-
nimmt. Damit kommen aus dieser Gruppe auch
nach 4 Jahren noch wesentliche Überschüsse,
so dass ein Abkappen zu grob falschen CLVs
führt. Die durchgeführte Begrenzung der Analy-
se aller Kundengruppen auf einen bestimmten
Zeitraum darf bei unterschiedlichen Retention
Rates nicht durchgeführt werden.
Sonstige Fehler
Nur am Rande sei erwähnt, dass die Rundungen
inkonsistent vorgenommen werden. Einige Be-
träge werden mit gerundeten Abzinsungsfak-
toren gerechnet, andere ohne Abrundung. Es
geschätzt werden, wie sich die Auszahlungen
im Zeitablauf ändern werden. Wenn z. B. mit ei-
ner erhöhten Auslastung gerechnet wird, so
sollten die Auszahlungen pro Kunde durch den
Fixkostendegressionseffekt fallen. Auch in die-
sem Fall wird aus Gründen der Vergleichbarkeit
angenommen, dass sich die Auszahlungen li-
near zu den Einzahlungen verändern, was aber
überprüft werden müsste. Der Einzahlungs-
überschuss in t=5 von 236,90 €
5
wird in den
Folgejahren durch die Retention Rate weiter fal-
len. Der Gesamtwert aller Überschüsse ab Pe-
riode 5 kann nun mit der Formel des Terminal
Values berechnet werden. Sie fasst alle Über-
schüsse von t=5 bis unendlich im Zeitpunkt
t=4 zusammen:
TV
4
= CF
5
* 1 / (wacc – g)
in €
4
TV
4
: Terminal Value: Wert aller Überschüsse/
Cashflows ab t=5 zum Zeitpunkt t=4
CF
5
: Überschuss im Zeitpunkt t=5
wacc: Weighted Average Cost of Capital
(Kalkulationszinssatz)
g:
Wachstumsrate (Growth Rate)
Die Wachstumsrate ist im Beispiel negativ mit
25 %, weil annahmegemäß jedes Jahr 25 %
der Kunden verloren gehen. Mit den Daten er-
gibt sich:
TV
4
= 236,90 * 1 / (0,1 - - 0,25) = 236,90 /
0,35 = 676,85 €
4
Da jedoch der heutige Wert der zukünftigen
Überschüsse ermittelt werden soll, muss noch
um 4 Jahre auf den Zeitpunkt t=0 abgezinst
werden. Das ergibt dann einen Wert von:
TV
0
= 676,85 €
4
/ ((1+wacc)
4
€
4
/ €
0
) = 462,30 €
0
Dieser auf t=0 bezogene Terminal Value TV
0
kann nun zur Barwertsumme der ersten 4 Peri-
oden von 1.355,87 €
0
addiert werden, so dass
schlossen werden, die unterjährig nicht gekün-
digt werden können. Wenn das nicht der Fall
ist, müsste z. B. in Quartalen gerechnet werden
und dann wieder hochgezinst werden. Proble-
matisch sind im Beispiel auch die Annahmen
zur Anzahl der zu berücksichtigenden Perio-
den. Nach 4 Perioden wird einfach abgebro-
chen, obwohl über die Retention Rate eine
bessere Vorgehensweise möglich ist. Da Mef-
fert/Bruhn/Hadwich drei unterschiedliche Kun-
dentypen mit unterschiedlichen Retention Ra-
tes betrachten, führt ein Abbruch der Kalkulati-
onen nach 4 Jahren zu unrealistischen Ergeb-
nissen. Es spricht nichts dagegen, die gleiche
oder eine angepasste Retention Rate weiter-
laufen zu lassen. Dazu muss der Wert aller
Überschüsse nach Ende der ersten 4 Jahre be-
rechnet werden. Die Kalkulation kann parallel
zum Terminal Value in der Unternehmensbe-
wertung durchgeführt werden (vgl. z. B. Berk/
DeMarzo/Harford, S. 96 f.). Die Vorgehenswei-
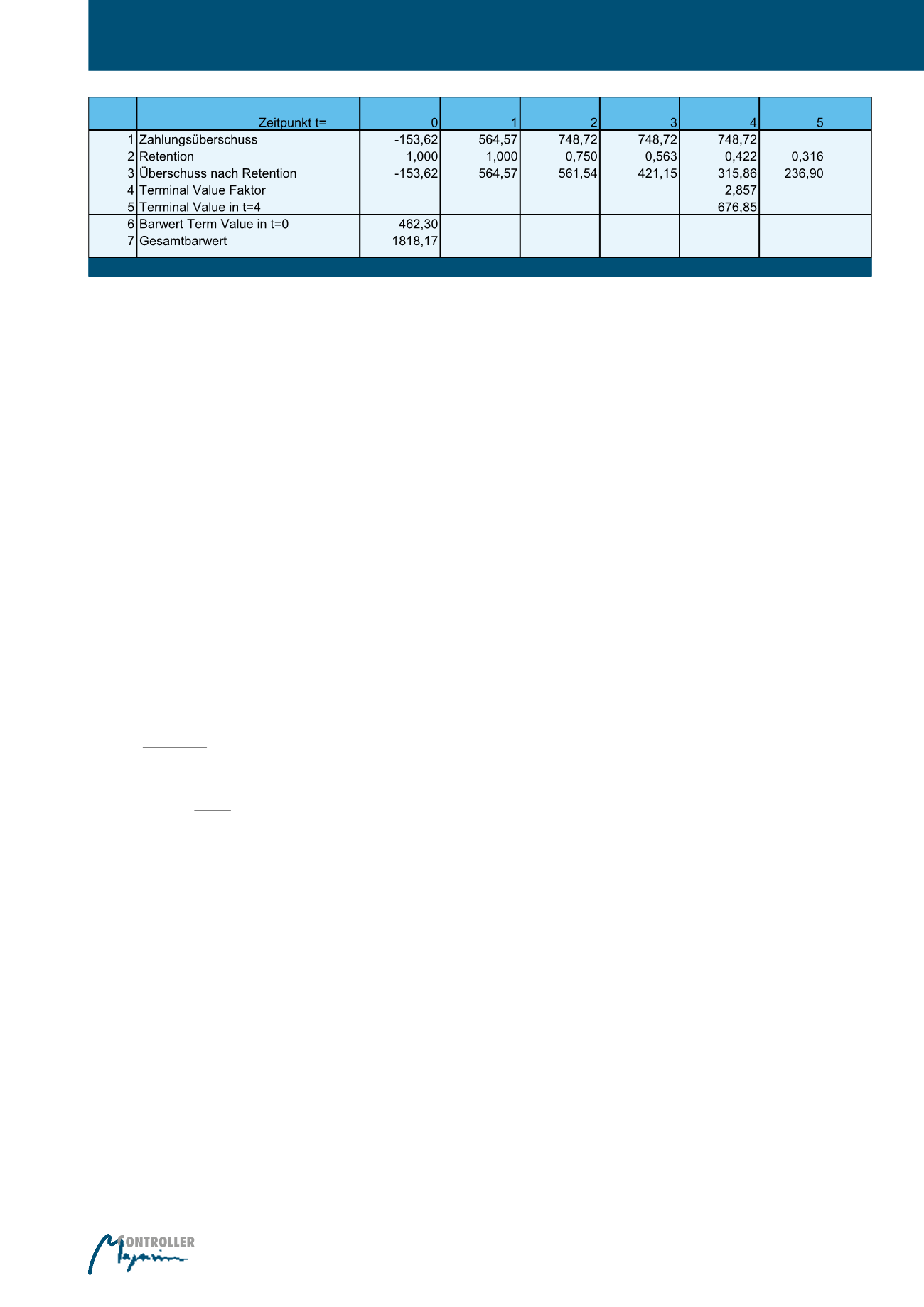
se wird in Abbildung 4 dargestellt.
In der ersten Zeile werden die Überschüsse der
ersten 4 Jahre aus Abb. 3, Zeile 4, übernom-
men. Im nächsten Schritt wird die Retention
Rate schon vor der Abzinsung berücksichtigt,
um die erwarteten Überschüsse pro Kunde im
Zeitablauf zu erhalten. Die Kalkulation wird für
den Zeitpunkt t= 5 fortgeführt, weil die Formel
für unendliche Zahlungen bei Wachstum eben-
so nachschüssig definiert ist wie übliche Bar-
wertfaktoren, d. h. sie bezieht sich auf den
Überschuss am Ende der ersten Periode der
untersuchten Perioden. In diesem Fall wird der
Wert gesucht, der nach t=4 noch generiert
wird. Es wird wieder die gleiche Retention Rate
verwendet, so dass die Einzahlungsüberschüs-
se in t=5 0,4219 * 0,75 * 315,86 = 236,90 €
5
betragen. Ohne Diskussion nehmen Meffert/
Bruhn/Hadwich in ihrem Beispiel an, dass auch
die verschiedenen Auszahlungsarten mit exakt
der gleichen Retention Rate zurückgehen. Das
wäre sicher ein großer Zufall. Eigentlich müsste
Abb. 4: Ermittlung des Gesamt-CLV ohne Abbruch nach 4 Jahren (Kundentyp 1)
Customer Lifetime Value


