33
mögliche Risikoauswirkung zwischen WC und
BC, mit Schwerpunkt um den MLC. Hier wer-
den in der Darstellung der WC, MLC und BC
mit einem Balken verbunden, um die Stetigkeit
der Verteilung zu symbolisieren. Der Erwar-
tungswert wird ebenfalls eingetragen (hier als
Raute) und liegt im gezeigten Beispiel außer-
halb der Schadensbandbreite, weil die Ein-
trittswahrscheinlichkeit des Risikos in diesem
Fall nur 20% beträgt.
Diese Darstellung benötigt nur eine Zeile pro
Risiko, so können in der Regel alle relevanten
zu berichtenden Risiken untereinander auf einer
Seite gezeigt werden. Bei dieser Übersichts
darstellung stellt sich dann die Frage nach der
Priorisierung bzw. Auswahl der Risiken.
Risikopriorisierung nach
Erwartungswert und Bandbreite
In der traditionellen Risk Map werden Risiken
über die Farbbereiche priorisiert. Durch loga-
rithmische Definition der Achsen wird hier häu-
fig eine Einteilung in etwa nach dem Erwar-
tungswert der Risiken erreicht, zumindest für
die Szenario-Risiken
4
. Der Erwartungswert ist
sicher ein sinnvolles Kriterium für die Priorisie-
rung, das bei der bandbreitenbasierten Risiko-
grafik ebenfalls angewendet werden kann, weil
der Erwartungswert alle möglichen Ausprägun-
gen des Risikos, gewichtet mit der jeweiligen
werden. Bei Chancen werden «blinde Fle-
cken» vermieden, da sie eindeutig über das
Upside priorisiert werden, s. u.
4) Das aggregierte Gesamtrisiko kann auf die
gleiche Art und Weise dargestellt werden wie
die einzelnen Risiken. Dadurch lassen sich
bereits grafisch die Beiträge der relevanten
Risiken zum Gesamtrisiko überschlagsmäßig
nachvollziehen, z. B. über die Fragen «Um
wie viel ist die Bandbreite des Gesamtrisikos
grösser als die des grössten einzelnen
(Bandbreiten-)Risikos?» oder «Welchen Bei-
trag liefern die drei größten Gefahren zum
Erwartungswert des Gesamtrisikos?»
Aufbau und Beschreibung
Die neue Darstellung bildet die gesamte Band-
breite der Risiken ab. Dafür werden pro Risiko
bis zu 4 Parameter bestimmt: Worst Case
(WC), Most Likely Case (MLC), Best Case (BC)
und der Erwartungswert. (Eine Erweiterung
mit sechs Parametern wird im Umsetzungs-
beispiel mit Excel vorgestellt). Risiken können
grundsätzlich mit diskreten und stetigen Ver-
teilungsfunktionen modelliert werden. Abbil-
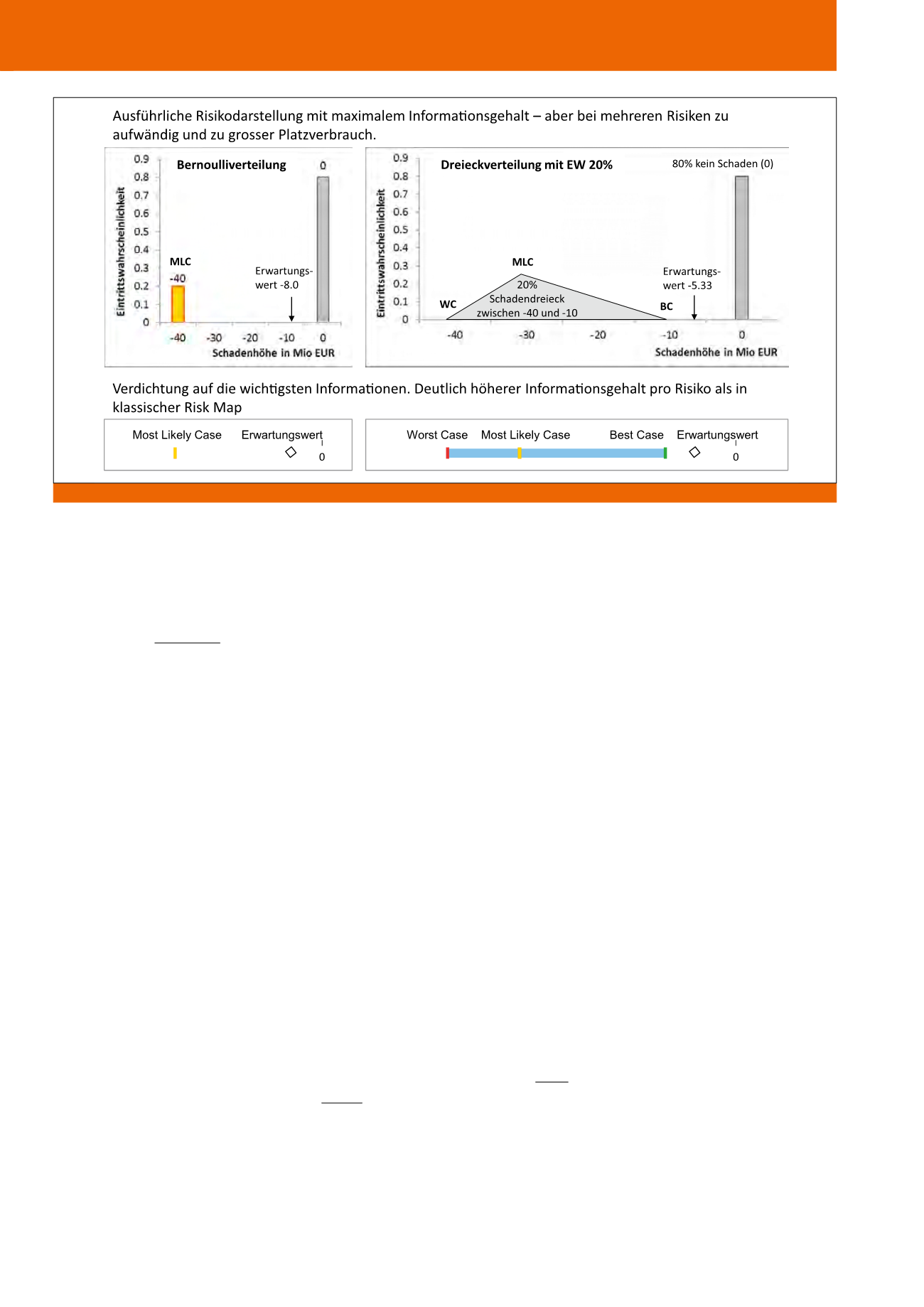
dung 3 verdeutlicht diesen Unterschied am
Beispiel einer typischen Bernoulli- und Drei-
ecksverteilung. Bei der Bernoulliverteilung gibt
es nur ein mögliches Risikoszenario (MLC) und
es werden der Erwartungswert und der MLC
dargestellt. Bei der Dreiecksverteilung liegt die
Bandbreitenbasierte Risikografik
als Lösung
Die bandbreitenbasierte Risikodarstellung ver-
meidet die beschriebenen Nachteile der traditi-
onellen Risk Map. Abbildung 2 zeigt beispiel-
haft eine solche Darstellung. Die Reihenfolge
der Risiken erfolgt hierbei nach dem Erwar-
tungswert. So werden die Risiken übersichtlich
unterteilt in Gefahren (negativer Erwartungs-
wert), Volatilitäten (Erwartungswert null) und
Chancen (positiver Erwartungswert).
1) Da für jedes Risiko die gesamte Bandbreite
kommuniziert wird, geht keine Information
verloren und die Risikoerfasser werden nicht
dazu verleitet, sich auf einen einzigen Punkt
oder auf ein einziges Risiko-Szenario festzu-
legen.
2) Die Notwendigkeit für Regeln, wie Bandbrei-
ten-Risiken (insbesondere Marktrisiken) mit
einem einzigen Punkt dargestellt werden,
entfällt. Somit gibt es keine ungewollte «Ver-
fälschung» in der Darstellung bzw. keine
Grenzfälle, für die die Regeln eher unglück-
lich sind.
3) Die Risikopriorisierung erfolgt für alle Risiken
nach dem (mathematisch korrekten) Erwar-
tungswert und gleichzeitig nach den Enden
der Bandbreite (z. B. VaR). Die Risiken kön-
nen über den Erwartungswert sortiert und so
in eine plausible Reihenfolge für die Darstel-
lung nach Gefahren und Chancen gebracht
Abb. 3: Bandbreitenbasierte Darstellung einer Bernoulliverteilung und Dreieckverteilung (Quelle: Axpo)
CM Juli / August 2019


