40
2. Eine Geldaufnahme in der Zukunft kann auf-
grund der Arbitragefreiheit mit zwei Kassa-
geschäften nachgebildet werden. Um eine
Kreditaufnahme in drei Jahren für ein Jahr
darzustellen, sind folgende Kassageschäfte
nötig: Aufnahme eines Kredites für vier Jah-
re und Anlage des Geldes für drei Jahre. Der
summierte Cashflow entspricht genau einem
Forward-Kredit für ein Jahr in drei Jahren.
Die Notation für Forwardgeschäfte folgt da-
her auch folgenden Schema: 3x4 (sprich
„drei gegen vier Jahre“). Aus diesen Cash-
flows kann dann der Forward-Zinssatz be-
rechnet werden.
Als Beispiel benötigt Ihr Manager verschiedene
Zinssätze von Ihnen, da eine Projektfinanzie-
rung in vier Jahren ausläuft und prolongiert
werden soll. Der Manager könnte sich die Zins-
kondition am Geld- und Kapitalmarkt sichern,
doch ist im Unternehmen noch nicht klar, wie
lange die Finanzierung verlängert werden soll.
Für Planungszwecke und um verschiedene
Szenarien rechnen zu können, erstellen Sie
eine zehnjährige Zinskurve ab dem Jahr vier.
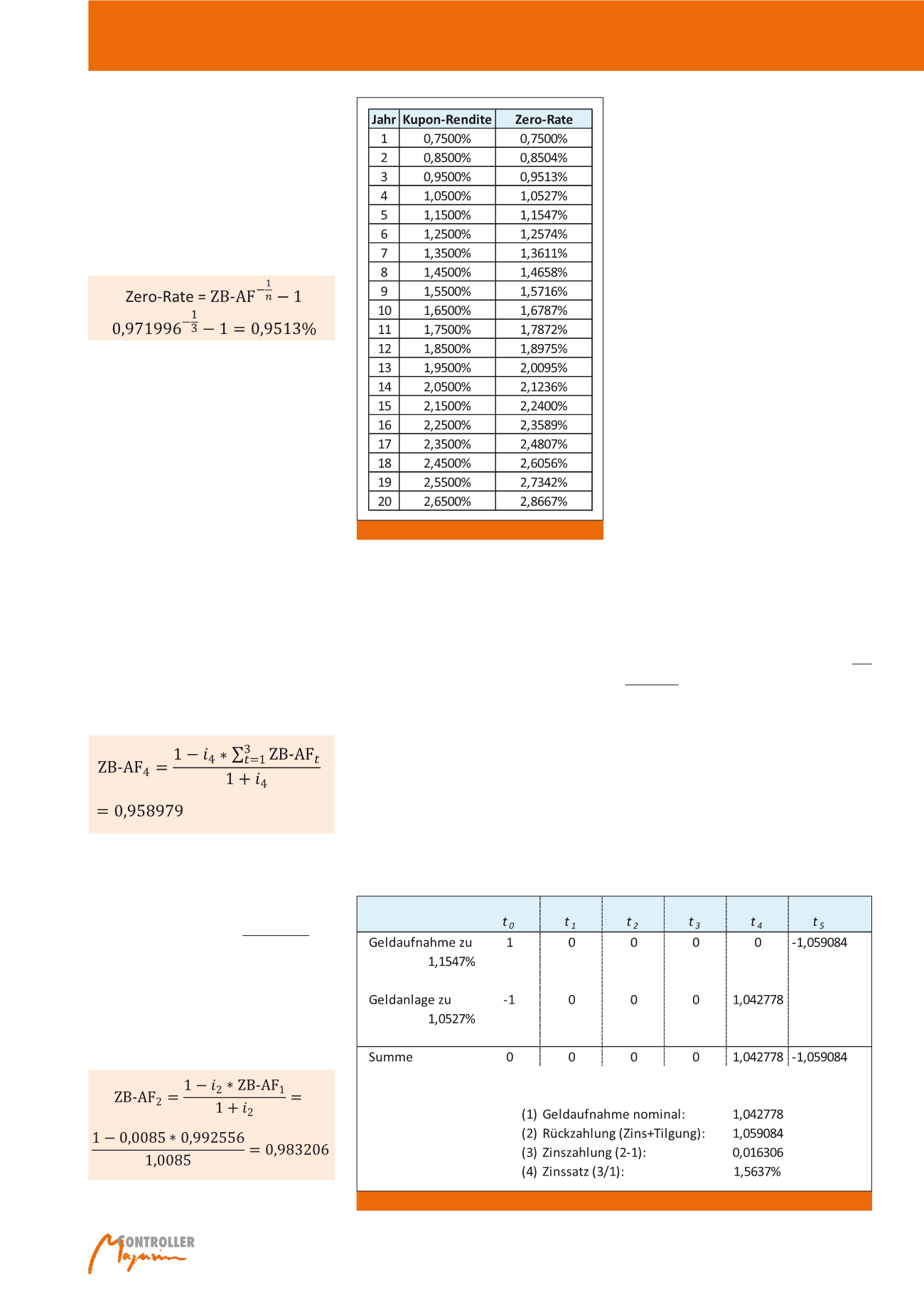
Die Cashflows der Kassageschäfte sind in Ab-
bildung 4 dargestellt. Damit aus den Cash-
flows leichter ein Zinssatz errechnet werden
kann, benutzt das Beispiel einen Nominalbetrag
von 1 €. Zuerst wird für fünf Jahre Geld aufge-
nommen zum Zero-Satz von 1,1547%. In fünf
Jahren ist dann ein Rückzahlungsbetrag von
1,059084 € fällig (1 * (1 + 0,011547)
5
). Das in
t
0
erhaltene Nominal aus dem Kredit wird eben-
falls in t
0
angelegt, jedoch nur für vier Jahre mit
einem Zero-Satz von 1,0527 % und führt zu
Berechnung der Forward-Sätze
Nachdem wir eine Zinskurve der Zero-Rates
hergestellt haben (auch Zero-Curve genannt),
geht es jetzt an die Berechnung der Forward-
Zinssätze. Dazu machen wir uns
zwei weitere
Prämissen
zu Nutze:
1. Alle Informationen, die der Kapitalmarkt
über die zukünftigen Zinssätze hat, sind in
der Zinskurve enthalten. Rechnen die
Marktteilnehmer zum Beispiel mit einer
Zinserhöhung in drei Jahren, spiegelt der
Zinssatz für vier Jahre das höhere Zins-
niveau im vierten Jahr wider.
von 1 € unter Berücksichtigung der aktuellen
Zinsstrukturkurve neutralisiert. Da wir das mit
einem Betrag von 1 € gemacht haben, ist das
auch gleichzeitig der ZB-AF. Aus diesem ZB-AF
müssen wir nun nur noch die Zero-Rate für drei
Jahre berechnen:
Formel 2:
Der Unterschied zwischen dem dreijährigen
Kupon-Zins und der dreijährigen Zero-Rate
sieht vernachlässigbar aus, aber bei einer
stärker gekrümmten Kurve oder bei großen
Beträgen kann das durchaus einen Unter-
schied machen. Damit wir nicht jede Laufzeit
mühsam nachkonstruieren müssen, bedienen
wir uns eines kleinen Tricks: Wir rechnen wie-
der rekursiv und zwar benutzen wir die bereits
errechneten ZB-AF, um nicht die einzelnen
Zinszahlungen jedes GKM-Geschäfts in den
früheren Perioden berücksichtigen zu müssen.
Zu den bekannten Zahlungsströmen aus den
bisherigen ZB-AF wird nur noch ein weiteres
Jahr hinzugefügt. Für das vierte Jahr sähe die
Formel wie folgt aus:
Formel 3:
Auch hieraus wird wieder die Zero-Rate be-
rechnet mit 0,958979
(-¼)
-1 = 1,0527%. Diese
Berechnung wiederholen wir für jede Laufzeit
und erhalten die Kurve aus Abbildung 3. Die
Zero-Rate für t
1
ist gleich der Kupon-Rendite,
der ZB-AF lässt sich entsprechend einfach als
Kehrwert von (1 + ZB - AF) schreiben. Für t
2
gilt
bereits Formel 3.
Formel 4:
Abb. 3: Zinskurven-Vergleich (mit Zero-Curve)
Abb. 4: Zinskurve ab Jahr 4
In die Zukunft sehen


