39
Alles, was wir dafür brauchen, ist eine Zinskur-
ve und etwas Mathematik.
Zinskurven bilden
die Zinssätze für verschiedene Laufzeiten
ab
und berücksichtigen damit unterschiedliche
Zinshöhen zu unterschiedlichen Zeitpunkten.
Die Forward-Rates stecken daher in den Zins-
sätze der Zinskurve drin, da ein Zinssatz für
eine zehnjährige Laufzeit
auch den Zeitraum
„in fünf Jahren für fünf Jahre“ beinhaltet
.
Doch wo kriegt man eine Zinskurve her? Es gibt
für fast jedes Finanzinstrument eine eigene
Zinskurve, wobei die meisten sich auf eine Kur-
ve mit quasi risikolosen Zinssätzen stützen.
Die
Zinskurven für deutsche Bundesanleihen
und Bankdarlehen unterscheiden sich zum
Beispiel in der Risikoanpassung
, die die
Bank für Darlehen vornimmt. Bildlich gespro-
chen ist die Darlehenskurve gegenüber den
Bundesanleihen nach oben verschoben. Um
nun Zinskurven für unterschiedliche Finanzinst-
rumente ermitteln zu können,
verwenden wir
eine Zinskurve für quasi risikofreie deut-
sche Bundesanleihen als Basis, um dann
mit Hilfe von Aufschlägen (Spreads) die be-
nötigte Kurve für das jeweilige Finanzinst-
rument
modellieren zu können.
Die Verwendung von deutschen Bundesanlei-
hen hat noch einen Vorteil: Diese Daten sind re-
lativ einfach verfügbar. Die Deutsche Bundes-
bank veröffentlicht auf ihrer Homepage täglich
aktuelle Zinskurven, zusätzlich sind diese Infor-
mationen auch auf den üblichen Finanzportalen
im Internet zu finden. Die Zinssätze dieser Zins-
kurven beziehen sich auf Anleihen mit
einer
jährlichen Zinszahlung (daher auch Kupon-
Zinssätze
). Für die Beispiele in diesem Artikel
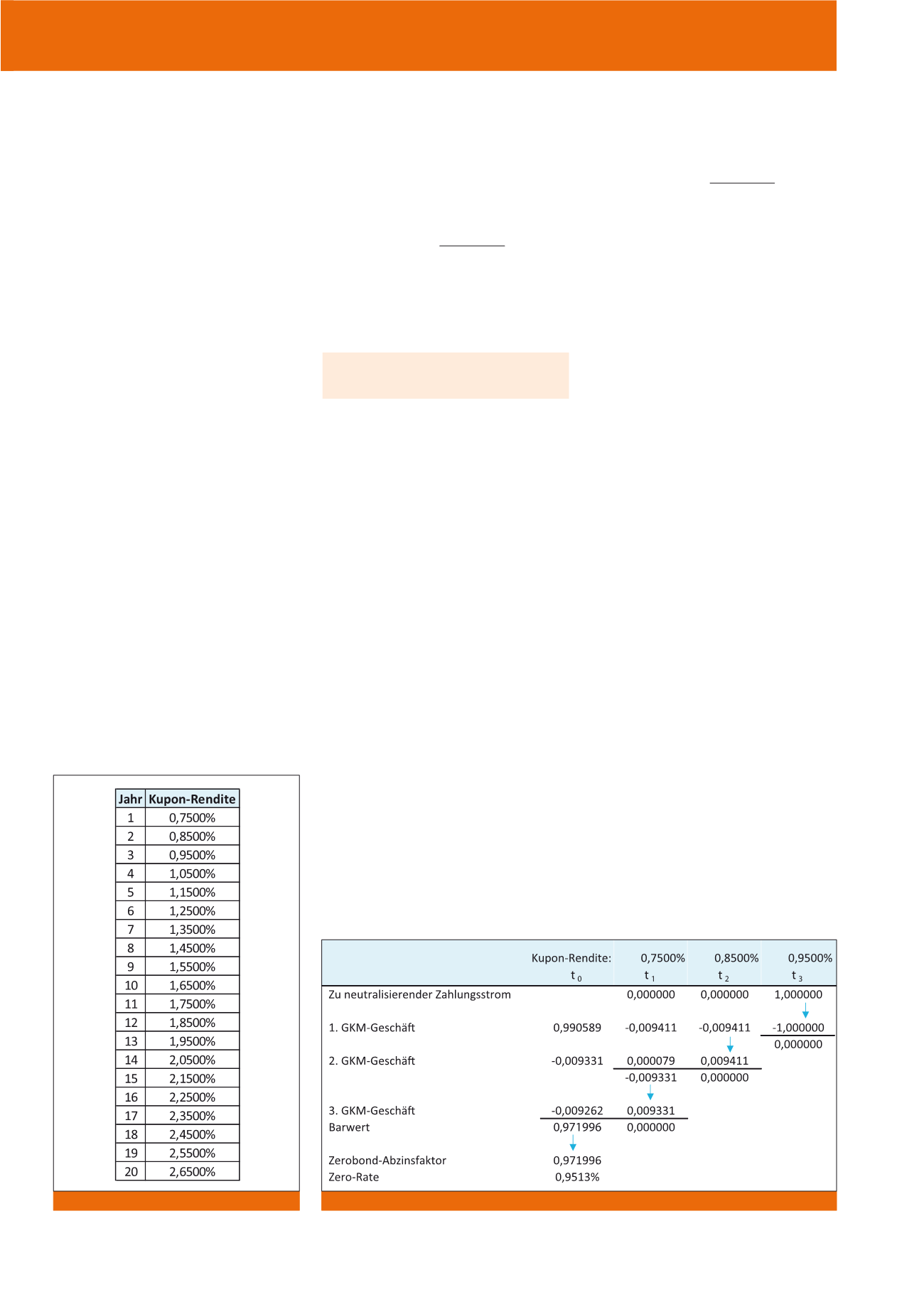
wird die Zinskurve in Abbildung 1 verwendet.
Der Endwert einer Anleihe mit 100 € Nominal-
wert und 3 Jahren Laufzeit wird mit der be-
kannten Zinseszins-Formel ermittelt:
Formel 1:
C
3
= C
0
* (1+i)
n
102,88 = 100 * (1 + 0,0095)
3
Berechnung der Zero-Rates
Diese Formel geht von einer
Wiederanlage-
prämisse aus
, die jährlichen Zinserträge in t
1
und t
2
können wieder zum Zinssatz i angelegt
werden. Diese Prämisse ist jedoch nur bei einer
flachen Zinsstrukturkurve erfüllt, die in der Re-
alität so gut wie nie vorkommt. Damit die Struk-
tur, also unterschiedliche Zinssätze für unter-
schiedliche Laufzeiten, berücksichtigt werden
kann,
rechnen wir zuerst die Kupon-Zins-
sätze in Nullkupon-Zinssätzen
(Zero-Rates)
um. Bei Nullkuponanleihen gibt es nur einen
Zahlungsstrom am Ende der Laufzeit, und es
fallen keine Zahlungen während der Laufzeit an
– jedoch weiterhin unter Berücksichtigung des
Zinseszins-Effekts. Um aus einem Kupon-Zins
eine Zero-Rate zu ermitteln, müssen wir zuerst
den
Zerobond-Abzinsfaktor (ZB-AF)
ermit-
teln. Der ZB-AF entspricht dem Kapitalwert C
0
,
der benötigt wird, um in Zukunft einen Zah-
lungsstrom von 1 € zu erhalten. Um diesen Ka-
pitalwert zu erhalten, bilden wir genau die
Cashflow-Struktur eines Zerobonds nach. Auf-
grund der Prämisse von arbitragefreien Kapital-
märkten muss ein Zerobond mit Kuponanleihen
nachzustellen sein. In Abbildung 2 ist dies für
die Laufzeit drei Jahre dargestellt, jedoch mit
Geschäften am Geld- und Kapitalmarkt (GKM-
Geschäft) anstatt Anleihen.
Die GKM-Geschäfte müssen einen Zahlungs-
strom neutralisieren, der nur zum Zeitpunkt t
3
1 € erzeugt, da aufgrund der Arbitragefreiheit
beide Geschäfte addiert genau 0 ergeben müs-
sen. Die Konstruktion der Zahlungsströme er-
folgt dabei rekursiv. Die erste Zahlungsreihe
muss in t
3
einen Zahlungsstrom von -1 € erzeu-
gen. Dazu wird in t
0
ein Kredit aufgenommen
in Höhe von 1 : 1,0095 , also 0,990589 €. Ach-
tung:
Das ist nicht das gleiche wie diskontieren!
Es wird nur der Auszahlungsbetrag eines Kredi-
tes gesucht, bei dem der Nominalbetrag plus
Zinsen eine Auszahlung von 1 € ergeben.
Diese Geldaufnahme erzeugt auch in t
1
und t
2
Zahlungsströme, nämlich die Zinsen. Um die
Zinszahlung in t
2
von -0,009411 € zu neutrali-
sieren, wird für 2 Jahre Geld angelegt, und
zwar so viel, dass nach zwei Jahren bei einem
Zinssatz von 0,85 % genau 0,009411 €
zurückfließen: (-0,009411) : (-1,0085) =
0,009331 €.
Damit sind die Zahlungsströme in t
2
neutrali-
siert, jedoch ist in t
1
eine weitere Zinszahlung
entstanden. Der gesamte Cashflow in t
1
von
0,009331 € wird durch ein drittes GKM-Ge-
schäft neutralisiert: Anlage von 0,009262 €
(= 0,009331 : 1,0075). Addieren wir nun alle
Zahlungsströme in t
0
, erhalten wir den Barwert
einer Zahlungsreihe, die einen Cashflow in t
3
Abb. 1: Zinskurvenbeispiel
Abb. 2: Tabellen-Modell für Zerobond-Abzinsungsfaktor
CM Juli / August 2017


