30
tragsschwachen Produktlinie ergab. Diese Pro-
duktlinie war jedoch für zwei A-Kunden nicht
unwichtig. Hätte man diese Linie aufgegeben,
wären mit Sicherheit wichtige Kunden verärgert
gewesen, wenn nicht sogar verloren gegangen.
Zwei zentrale Hürden sind bei der Optimie-
rung zu umschiffen
; diese werden im Folgen-
den dargestellt als Voraussetzungen für die
Nutzung von Optimierungsrechnungen in der
Unternehmensplanung:
Hürde 1: Das mathematische Modell muss
zeitnah und wirtschaftlich „gewartet und
betrieben“ werden können.
Bis vor einigen Jahren waren noch gar nicht die
notwendigen Datenverarbeitungsmöglichkeiten
vorhanden, um Optimierungsmodelle adäquat
zu handhaben. Franke (Reimund Franke: „Be-
triebsmodelle: Rechensysteme für Zwecke der
kurzfristigen Planung, Kontrolle und Kalkula-
tion“, Bertelsmann-Universitätsverlag, Düssel-
dorf 1972) erstellte bereits im Jahre 1972 das
Modell einer vektorbasierten Optimierungs-
rechnung für ein Stahlwerk, das 88 Kostenar-
ten von acht Kostenstellen in ihrer Auslastung
kostenoptimal kombiniert. Letztlich benötigte
das Aktualisieren des mathematischen Modells
jedoch so viel Zeit und Aufwand, dass sich ein
dauerhafter Betrieb als unwirtschaftlich erwies.
Doch das ist heute anders.
Nebenbedingung könnte z. B. die Annahme
sein, dass der Start- und Zielort eines jeden
Wagens identisch ist. In einem anderen Szena-
rio können die
Nebenbedingungen variiert
werden
. Beispielsweise kann man davon aus-
gehen, dass es mehr als einen Standort gibt
und die Fahrzeuge über unterschiedliche De-
pots verteilt sind.
Die sich aus der Optimierung ergebenen Rou-
ten und Zahlen eines jeweiligen Szenarios
können dann in einem nachgelagerten Analy-
sesystem weiter bewertet und hinterfragt wer-
den. Mathematisch sind diese Fragestellun-
gen viel komplexer als einfache lineare Opti-
mierungsprobleme. Doch auch hierfür existie-
ren sehr leistungsfähige Lösungsverfahren,
die in sehr vielen Fällen ausreichend schnell
sehr gute oder sogar optimale Lösungen be-
rechnen können.
Hürden des Einsatzes von
Optimierungsmodellen
Es gibt wohl kaum ein Unternehmen, das nicht
ein Fallbeispiel einer gescheiterten Optimie-
rungsrechnung bringen kann. Ein Industrieun-
ternehmen berichtete beispielsweise davon,
dass das Ergebnis einer Deckungsbeitragsopti-
mierung die Aufgabe einer relativ deckungsbei-
handene Ressourcen werden zu Nebenbedin-
gungen und die Anzahl der gefertigten Produkte
wird zur Zielfunktion. Zur Lösung nutzt man oft
das sogenannte
Simplex-Verfahren
, das zu
den linearen Optimierungsverfahren zählt. The-
oretisch kann die Rechenzeit des Simplex-Ver-
fahrens exponentiell steigen. In der Praxis zeigt
sich aber immer wieder, dass Simplex schnell zu
einem Ergebnis führt. Das Ergebnis ist dann
entweder eine Lösung oder die Aussage, dass
das Optimierungsproblem nicht lösbar ist.
Besonders interessant für die Praxis sind auch
Fragestellungen, bei denen lineare Optimie-
rungsprobleme mit Entscheidungen kombiniert
werden (sogenannte gemischt-ganzzahlige
lineare Optimierungsprobleme). Im Transport-
bereich wie bei der Post oder bei der Bahn geht
es zum Beispiel um
Tourenplanungen, wo
die Transporte hinsichtlich ihrer Transport-
wege optimiert werden.
Um das Problem zu
lösen, kombiniert man zwei Aspekte: Cluste-
ring und Routen. Sendungen werden zusam-
mengefasst und Routen bezüglich ihrer anzu-
fahrenden Orte berechnet. Das Optimierungs-
ziel kann die Minimierung der Anzahl der ein-
gesetzten Fahrzeuge oder der zurückgelegten
Strecke sein.
Durch Abänderung der Nebenbedingungen las-
sen sich verschiedene Szenarien betrachten.
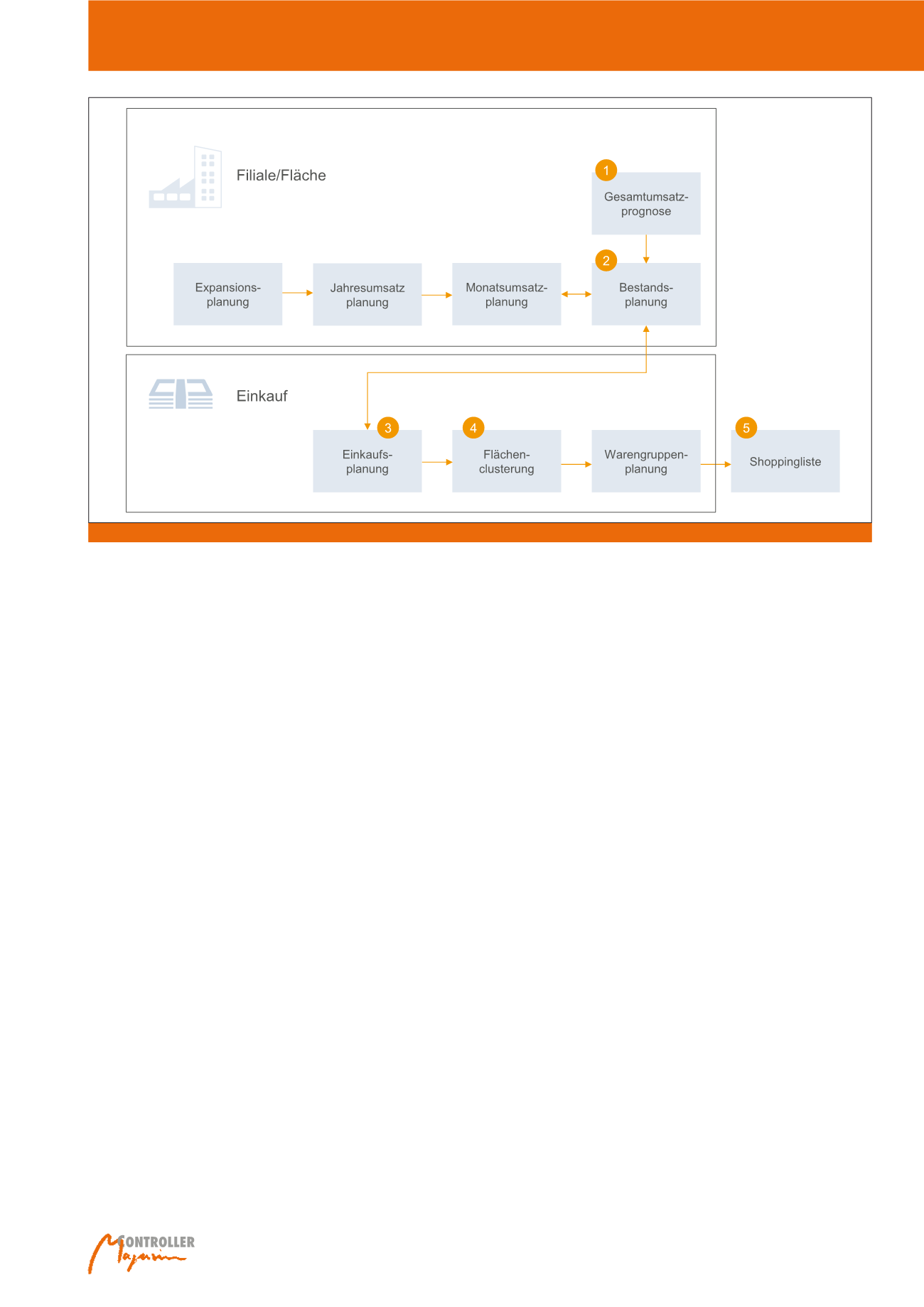
Abb. 2: Einsatzbereiche für Optimierungsrechnungen im Handelsbetrieb
Optimierung in der Planung


