63
welcher die Spanne noch 1 €/ME beträgt. In
Stufe 7 fällt der relevante Nettopreis um 1,5 €/
ME, so dass die Spanne mit -0,5 €/ME negativ
wird. Die Optimierung kann abgebrochen wer-
den, weil zusätzliche Mengen einen geringeren
relevanten Nettopreis bringen würden als ihre
Erstellung kosten würde. Der Gesamtdeckungs-
beitrag beträgt 1705 €/Pe. Dieser maximale
Wert basiert auf der Grenzmethode, indem nur
die Mengen und Spannen der ersten 6 Stufen
kalkuliert werden.
Man könnte nun argumentieren, dass es mög-
lich sei, für alle Mengen mit bestimmten Kosten
eine Absatzmöglichkeit zu finden, die einen hö-
heren relevanten Nettopreis aufweist. So könn-
te man z. B. für die letzte Produktionsmöglich-
keit 5 mit relevanten Stückkosten von 7 €/ME
und einer Menge von 90 ME/Pe die beste Ab-
satzmöglichkeit 1 mit relevanten Nettopreisen
von 10 €/ME einsetzen, so dass diese Produk-
tionsmöglichkeit vorteilhaft erscheint. Damit
würde man aber den Vorteil der ersten Stufen
verlieren. Der Deckungsbeitrag würde bei voll-
ständiger Produktion nur 1415 €/Pe betragen.
Dies wird auch aus der Abbildung 8 deutlich.
Ziel ist es, die Summe der Differenzen zu ma-
ximieren. In der Graphik sieht man noch einfa-
cher, dass der letzte sinnvolle Schritt im Über-
gang von 240 auf 260 ME/Pe vorliegt. Der
folgende Schritt auf 310 ME/Pe hätte dann
schon eine negative Spanne. Im Beispiel war
angenommen worden, dass jeweils ein Preis
in einer Vermarktungsmöglichkeit für eine
Menge gilt. Es mag aber nun sein, dass die
Menge vom Preis abhängt, was häufig mit ei-
ner Preisabsatzfunktion abgebildet werden
kann. Dann kann mittels des Grenzgewinns
ermittelt werden, welche Preise und Mengen
derungen an die Höhe des Vermarktungser-
folgs stellt. Die Daten mit den Vermarktungs-
möglichkeiten werden nun mit den Produkti-
onsmöglichkeiten „verheiratet“. Stufe 1: Auf
Basis der besten Vermarktungsmöglichkeit mit
maximal 100 ME/Pe wird die günstigste Pro-
duktionsmöglichkeit zugeordnet, welche 70
ME/Pe umfasst. Also kann zur Spanne von 10
– -0,5 = 10,5 €/ME nur das Minimum der bei-
den Mengen, also 70 ME/Pe, eingeplant wer-
den (vgl. Abbildung 7).
Damit bleiben dann in Stufe 1 noch 30 ME/Pe
zur Vermarktung über. Diese müssen durch die
nächste Produktionsmöglichkeit abgedeckt
werden, was dann in Stufe 2 geschieht. Die
Spanne sinkt auf 10 – 1 = 9€/ME. Da die Pro-
duktionsmöglichkeit 2 aber für 80 ME/Pe gilt,
verbleiben 50 ME/Pe in der letzten Spalte. Die-
se suchen dann in Stufe 3 ihre Absatzmöglich-
keit. Auf diese Weise werden nun immer neue
Absatz- bzw. Produktionsmöglichkeiten einge-
plant, solange die Spanne positiv ist. Denn
dann wird noch ein Wert für das Unternehmen
erzeugt. Dies gilt bis einschließlich Stufe 6, in
möge dies zeigen. In Abildung 5 sind zunächst
unterschiedliche Kunden bzw. Vermarktungs-
möglichkeiten aufgeführt, bereits in abfallender
Reihenfolge geordnet.
Die erste und beste Vermarktungsmöglichkeit
würde einen relevanten Nettopreis von 10 €/
ME generieren und würde maximal 100 ME in
der betrachteten Ausverkaufsperiode aufneh-
men. Wenn eine Produktionsmöglichkeit mit re-
levanten Kosten von unter 10 €/ME gefunden
werden kann, so würde die erste Vermark-
tungsmöglichkeit realisiert. Die relevanten Kos-
ten sind in der Abbildung 6 aufgeführt. Die
günstigste Quelle hat negative Stückkosten von
-0,50 €/ME, weil ihr Einsatz z. B. eine Vernich-
tung vermeiden würde. Sie gilt für 70 ME/Pe. In
Stufe 2 würden nur 1 €/ME anfallen für 80 ME
in der betrachteten Periode. Das könnte dann
der Fall sein, wenn ein Zwischenprodukt nur
noch wenige Transformationsschritte bis zur
Fertigstellung benötigt.
Die weiteren Stufen erfordern immer höhere re-
levante Stückkosten, was entsprechende For-
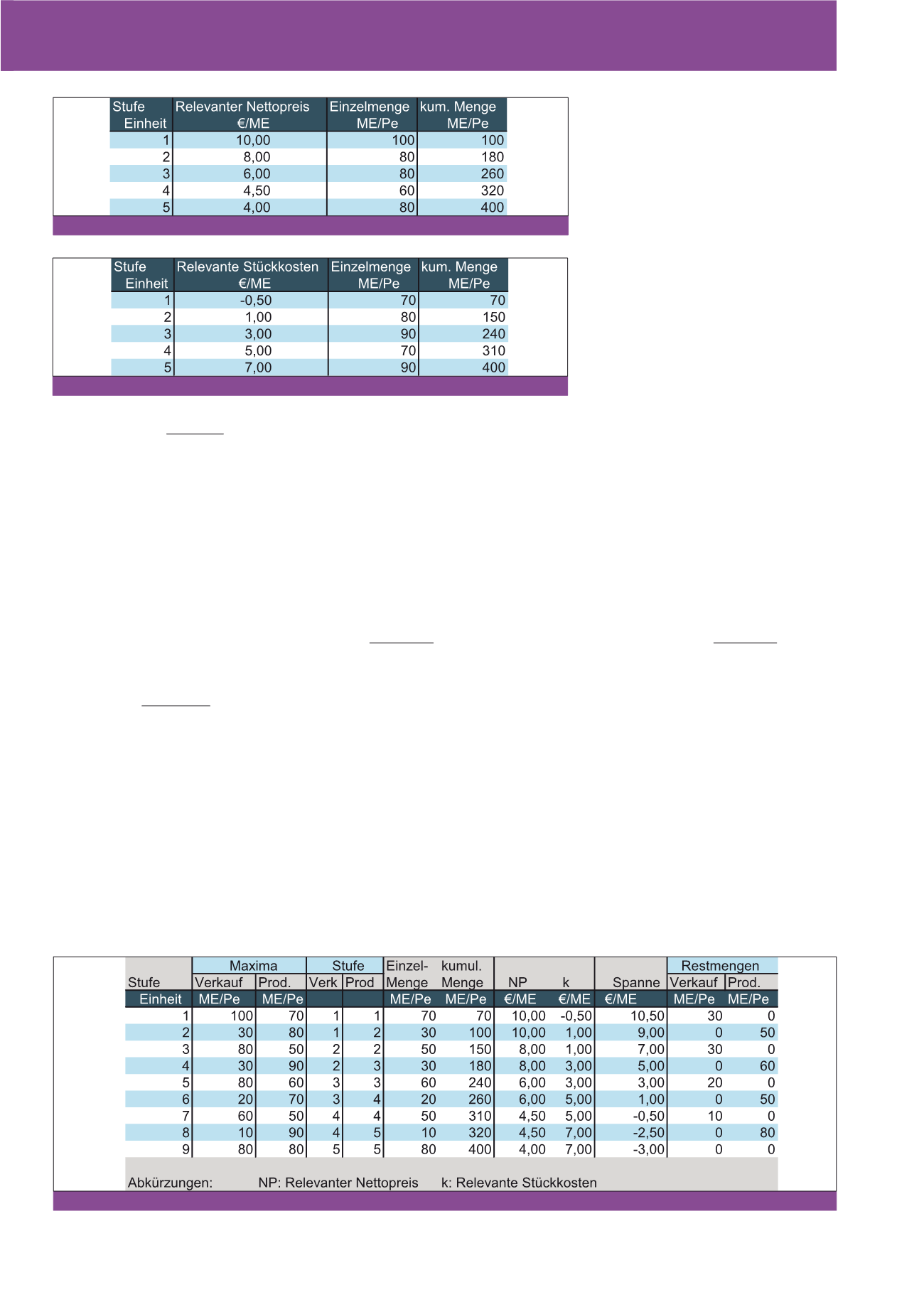
Abb. 5: Mögliche relevante Nettopreise mit Mengen
Abb. 6: Mögliche relevante Stückkosten mit Mengen
Abb. 7: Optimierungsschritte
CM November / Dezember 2016


