67
Sinne einer treiberbasierten Planung heißt das
aber, dass lediglich die festgelegten Treiber von
den Fachverantwortlichen geändert werden,
und es ergibt sich automatisch ein vollständiges
Set an Planzahlen, für jeden Bereich und für
das gesamte Unternehmen.
Insofern müssen
Annahmen für die Treiber einfach änderbar
sein und ein neuer „Forecast“ muss sich
ohne Eingreifen des Controllings auf
„Knopfdruck“ ergeben.
Und was ist dann ei-
gentlich die Aufgabe des Controllings? Anstatt
sich mit den Zahlen zu beschäftigen, geht es
darum, das bestehende Planungsmodell zu hin-
terfragen. Hat sich das Geschäftsmodell an der
einen oder anderen Stelle geändert? Sind neue
Ideen oder Maßnahmen hinzugekommen, die
für die Planung eine Rolle spielen? Welche Ent-
scheidungen sollen anhand der Planung getrof-
fen werden und wie können wir diese unterstüt-
zen? Insofern ist das Controlling für die Aktuali-
sierung und Erweiterung des Planungsmodells
zuständig und nicht für die Zahlen an sich, denn
die sind lediglich ein „Nebenprodukt“.
Das Pla-
nungsmodell muss daher schnell und indi-
viduell erweiterbar sein. Ich meine das
nicht im Sinne der Zahlen, sondern im Sin-
ne der Logik, mit der die Planzahlen be-
rechnet werden.
Es geht um Modellierung
und nicht um Konsolidierung. Außerdem muss
Planung immer als Instrument der Unterneh-
menssteuerung verstanden werden und des-
wegen die aktuellen Fragestellungen des Ma-
nagements aufgreifen und unterstützen. Wenn
eine Unternehmensplanung das leisten kann,
ist sie aus meiner Sicht beweglich, also agil.
Das richtige Werkzeug
Nun werden Sie mir vielleicht bei meinen Aus-
führungen zustimmen oder auch nicht, aber es
bleibt eine zentrale Frage offen: Wie macht
man das? Die richtige Softwareunterstützung
ist dabei ein zentraler Aspekt.
Statt einer
klassischen Planungssoftware, in der man
Zahlen erfasst oder konsolidiert, braucht
man dafür ein Werkzeug, mit dem man die
unternehmensspezifische Geschäftslogik
schnell und transparent in einem individu-
ellen Planungsmodell abbilden kann.
Inso-
fern muss das die Kernfunktionalität des Werk-
zeuges sein, denn nur damit kann der treiber-
basierte Planungsansatz umgesetzt werden.
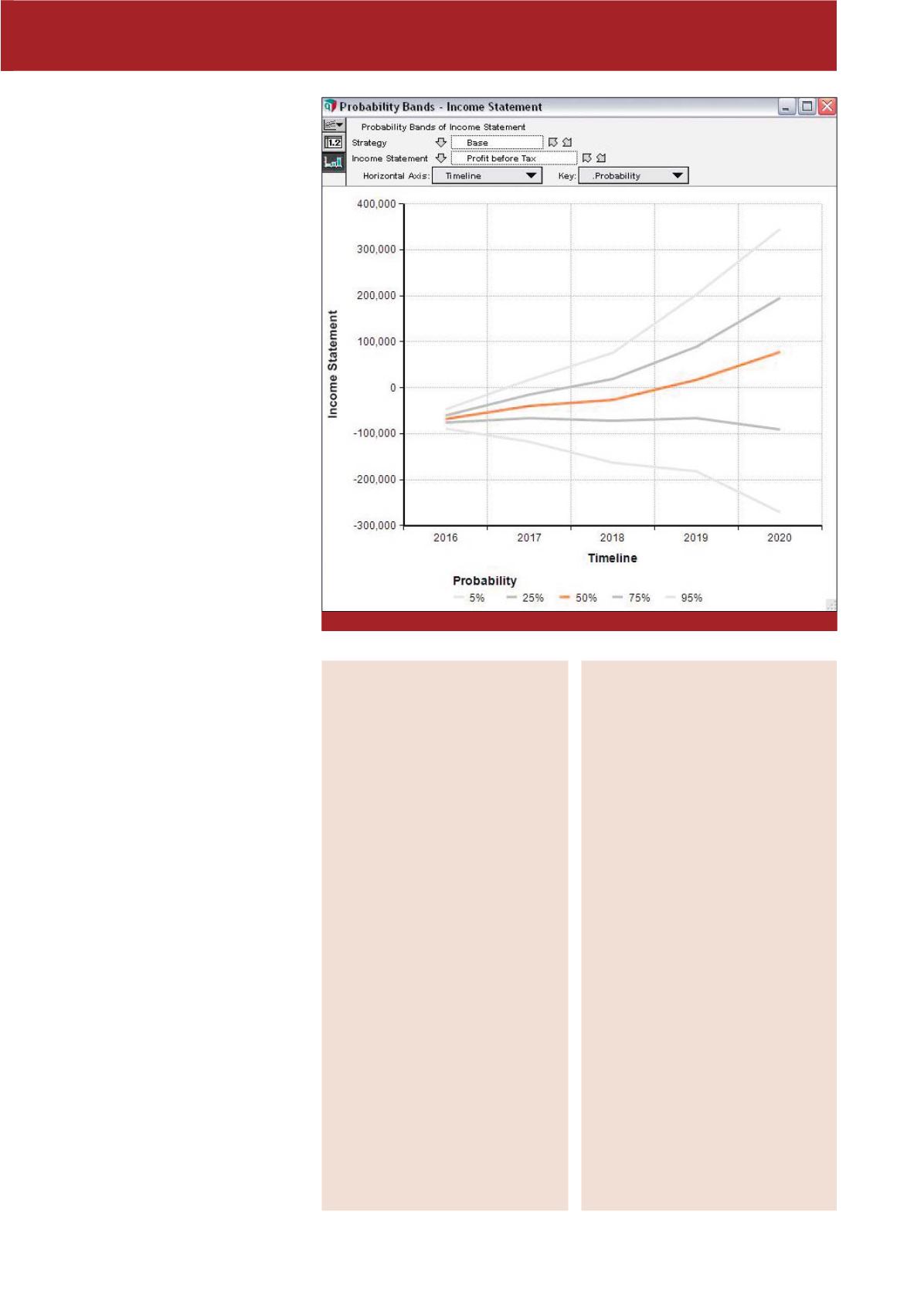
Abb. 4: Bandbreitenplanung
„Monte-Carlo-Simulation“
Wenn Sie bei Monte-Carlo-Simulation an
Casino denken, liegen Sie eigentlich ganz
richtig, denn auch hierbei geht es um Zu-
fallszahlen, die sich innerhalb eines Rah-
mens bewegen. Bei diesem statistischen
Verfahren geht es darum, aus verschiede-
nen Wahrscheinlichkeitsverteilungen jeweils
zufällig einen Wert zu ziehen, um daraus ein
Ergebnis zu berechnen. Diese „Ziehungen“
(Simulationsläufe) werden tausende Male
wiederholt, und es ergeben sich somit zufäl-
lig tausende Ergebnisse, die wiederum als
Häufigkeitsverteilung dargestellt werden.
Daraus können neben Mittelwerten auch
Wahrscheinlichkeiten abgelesen werden,
mit der ein bestimmtes Ergebnis eintritt. Also
zum Beispiel solche Aussagen: „Im Durch-
schnitt wird der Umsatz im nächsten Jahr
bei EUR 2,9 Mio. liegen. Mit einer Wahr-
scheinlichkeit von 80% wird der Umsatz
größer als 2,6 Mio. sein. Dass der Umsatz
größer als 3,5 Mio. sein wird, ist sehr un-
wahrscheinlich.“
„Wahrscheinlichkeitsverteilung“
Die wohl bekannteste Form einer Wahrschein-
lichkeitsverteilung wird Standardnormalver-
teilung genannt und war sogar auf dem letzten
10-DM-Schein abgedruckt. Wahrscheinlich-
keitsverteilungen (oder auch Häufigkeitsver-
teilungen) zeigen an, wie oft (also häufig) ein
bestimmter Wert vorkommt. Stellen Sie sich
vor, Sie würfeln tausend Mal, tragen jedes Er-
gebnis in eine Liste ein und am Ende würden
Sie zählen, wie oft eine bestimmte Augenzahl
erreicht wurde. Das Ergebnis können Sie auch
als Diagramm darstellen. Wenn Sie nur einen
Würfel haben, wird nach tausend Mal Würfeln
Ihr Diagramm ungefähr gleich große Balken für
jeden Wert von 1 bis 6 enthalten. Haben Sie
zwei Würfel, werden die Balken unterschiedlich
hoch, denn die Kombination 2 oder 12 ist
unwahrscheinlicher als die Kombination 7.
Unsichere Merkmalsausprägungen (Werte) und
Verteilungen gibt es nicht nur beim Würfeln,
sondern auch beim Lottospielen, bei Wechsel-
kursen, Rohstoffpreisen, Absatzmengen und
eigentlich allem, was irgendwie unsicher ist.
CM September / Oktober 2017


