70
de Gleichungen ableiten, wobei Formel 3 für
den Anstieg und Formel 4 für den Rückgang
des betreffenden Zinssatzes verwendet wird.
(3)
(4)
S
0
= Aktueller Zinssatz
Z = Z-Wert des Konfidenzintervalls
= Jährliche Standardabweichung
√T = Wurzel aus der Zeitspanne zwischen aktu-
ellem Zinssatz und erwartetem Zinssatz
Bei den meisten variablen Finanzierungen wird
der 3-Monats-EURIBOR als Referenzzinssatz
herangezogen. Je nachdem wie sich dieser
Zinssatz entwickelt, verändert sich auch der
Zinssatz der Finanzierung, welcher als Refe-
renzzinssatz plus Kreditaufschlag definiert ist.
5
Grundsätzlich verbleibt der Kreditaufschlag
gleich, kann sich jedoch je nach Risiko- und
Preispolitik der finanzierenden Bank ändern. In
der Praxis ist häufig zu beobachten,
dass bei
einer Ratingverschlechterung nicht sofort
eine Erhöhung des Kreditaufschlages er-
folgt.
Dasselbe ist aber auch bei einer Rating-
verbesserung zu beobachten, welche grund-
sätzlich auf Grund einer risikoadjustierten
Preispolitik eine Reduktion des Kreditauf-
schlags bedingen müsste. Der Aufschlag kann
somit allgemein als „statische“ Größe angese-
hen werden, welche sich nur in extremen Be-
dingungen verändert. Daher reicht es für die
Abschätzung der Finanzierungskosten aus, nur
die Veränderung des Referenzzinssatzes zu
taxieren. In Abbildung 3 ist der Verlauf des
3-Monats-EURIBOR für den Zeitraum 2010-
2013 dargestellt.
Ausgehend von diesen Daten kann berechnet
werden, dass der Mittelwert für diesen Zeit-
raum bei 0,75% lag, wobei eine Standardab-
weichung von 0,475% gege-
ben war. Der Wert des 3-Mo-
nats-EURIBOR per 31.12.2013
lag bei 0,288%. Ausgehend
von diesen Daten lässt sich
nun berechnen, wie sich der
3-Monats-EURIBOR innerhalb
einer bestimmten Bandbreite
entwickeln kann (vgl. Formeln
5 und 6).
Ein Beispiel für eine Anwendungsmöglichkeit ist
in Abbildung 2 zu sehen. VaR sagt in diesem
Fall aus, dass mit einer Wahrscheinlichkeit von
99% über einen Zeitraum von 6 Monaten der
Verlust aus dem Investment den Wert von
82.377,94 EUR nicht übersteigen wird.
(2)
Nutzung von VaR zur Abschätzung
von Zinsentwicklungen
Diese grundsätzlichen Überlegungen zum VaR
können auch für die Abschätzung von Zinsent-
wicklungen genutzt werden. Es ist dadurch
möglich, dass man Prognosen zur Entwicklung
von bestimmten Zinsindikatoren mit gewissen
Bandbreiten basierend auf den definierten Kon-
fidenzintervallen tätigen kann. Die Basis für
diese Berechnungen bietet VaR, wobei hier auf
eine lognormal verteilte Verteilung übergegan-
gen wird. Ausgehend davon lassen sich folgen-
über einen bestimmten Zeitraum mit einer be-
stimmten Wahrscheinlichkeit geben.
3
Bei der
Berechnung von VaR wird davon ausgegan-
gen, dass die Entwicklung der betrachteten
Parameter einer Normalverteilung folgt. Das
bedeutet somit, dass man für die Konfidenz-
intervalle die Z-Werte der Normalverteilung
verwenden kann. Bei einem Konfidenzintervall
von 95% ist dies 1,65 und für 99% 2,33. Die
Schwankungsbreite des Risikos ist über die
Standardabweichung einer Messreihe be-
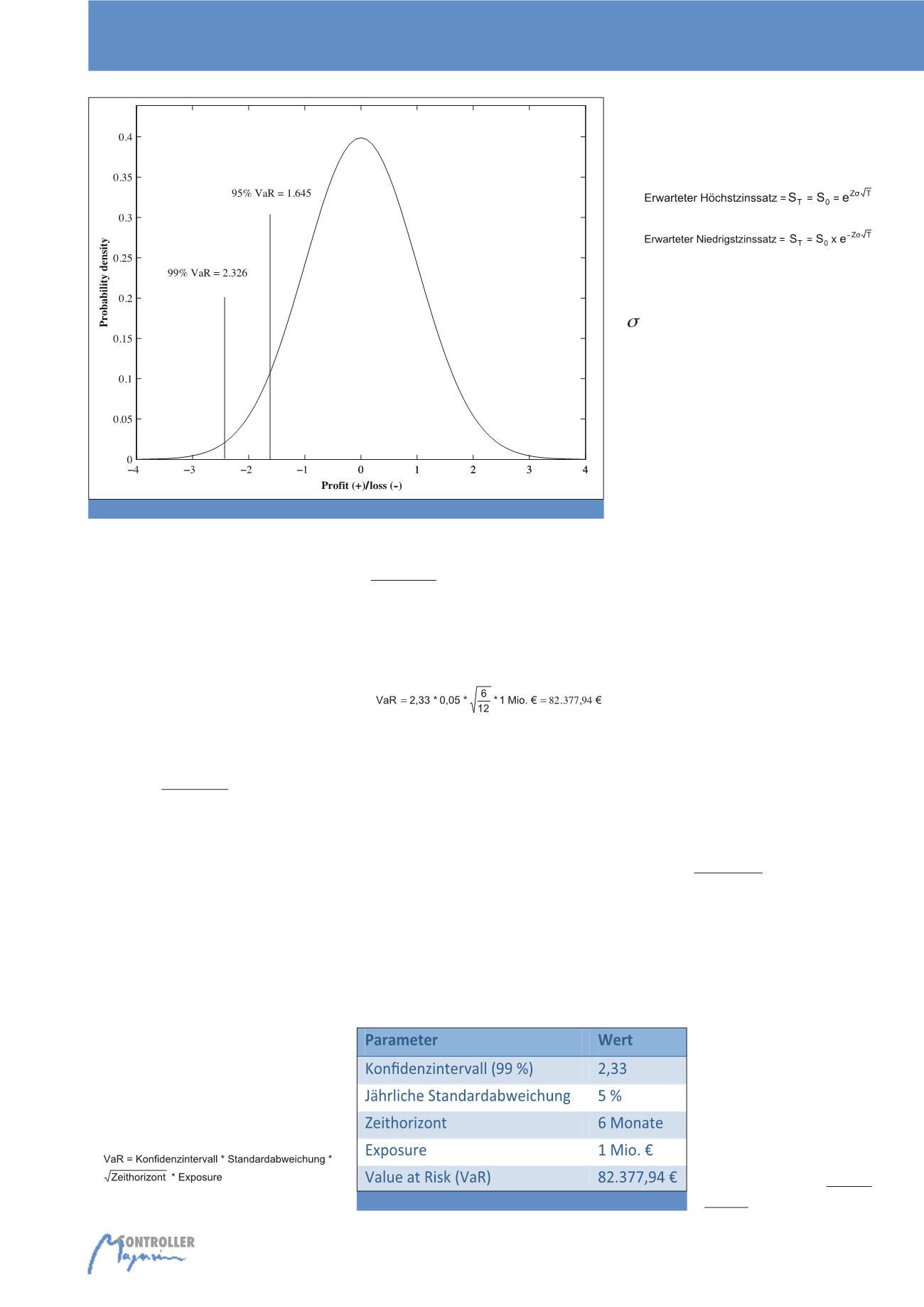
stimmbar. In Abbildung 1 ist das Wesen von
VaR dargestellt.
Die Abbildung zeigt eine Dichtefunktion der
Normalverteilung und die Konfidenzintervalle
des VaR für 95 und 99%. Wenn man bspw. den
VaR von 99% berechnet, dann bedeutet dies,
dass man den schlechtmöglichsten Ausgang
für dieses Konfidenzintervall berechnen kann.
Wichtig ist hierbei zu wissen, dass dies nicht
das „schlimmste Szenario“ darstellt. Es ist sehr
wohl zu 1% möglich, dass der effektive Verlust
höher ausfallen kann. Mit VaR lässt sich zumin-
dest eine Aussage treffen, dass der berechnete
Verlust zu 99% dem „schlimmsten Szenario“
entspricht. Die Gleichung für die Berechnung
von VaR ist in Formel 1 dargestellt.
(1)
Abb. 1: VaR und Normalverteilung
4
Abb. 2: Beispiel zur Berechnung von VaR
Planungssicherheit bei Finanzierungskosten


