44
den. Die Kalkulation soll für die Maßnahme 1 –
Erhöhung der Taktrate – dargestellt werden,
welche über 4 Jahre (Zeile 6) läuft. Die 4 Jahre
entsprechen 48 Monaten, in welchen die
400.000 €
0
mit Zins und Zinseszinsen zurück-
fließen müssen. Die Einheit €
0
enthält den Zeit-
index 0, um klar zu machen, wann die Zahlung
anfällt. Für Monatsraten wird die Schreibweise
€1;tn gewählt, um zu zeigen, dass die Euros
vom Ende des ersten Monats bis zum letzten
Monat kommen. Der letzte Monat t=tn weist im
Beispiel den Wert 48 auf. Es werden somit 48
Monatsraten gesucht, deren Barwertsumme
genau der Investitionssumme entspricht. Für
diese Berechnung werden Wiedergewinnungs-
faktoren verwendet (vgl. z. B. Varnholt/Hoberg/
Gerhards/Wilms, S. 88 ff.):
WGF
n
= (q
tn
* i) / (q
tn
-1)
in €
1;48
/ €
0
WGF
n
= Nachschüssiger
Wiedergewinnungsfaktor
i
= Monatszinssatz
q
= Monatszinsfaktor: 1+ i
tn
= Anzahl Monate (hier 48)
Wie die Einheit €
1;48
/ €
0
zeigt, gibt der Wieder-
gewinnungsfaktor an, welche 48 nachschüssi-
gen Monatsraten für jede Geldeinheit resultie-
ren, die in t=0 für die Investition angefallen ist.
Mit den Daten des Beispiels ergibt sich:
WGF
n
(tn=48; i
m
=0,797%) = 0,02516
in €
1;48
/ €
0
Anders ausgedrückt müssen jeden Monat
nachschüssig 2,516% der Investitionsauszah-
lungen zurückgezahlt werden (Zeile 7 in Abbil-
dung 3). Mit diesen Zahlen beträgt die monatli-
che Annuität der Entwicklungszahlungen
0.02516 €
1;48
/ €
0
* 400.000 €
0
= 10.062 €
1;48
.
Im nächsten Schritt sind die sonstigen monat-
lichen Kosten zu ermitteln, wofür in Abbildung
4 die entsprechenden Schätzwerte angege-
ben sind.
Die in Abbildung 4 aufgeführten Kosteneinspa-
rungen sind wieder einheitlich auf das Ende
des jeweiligen Monats bezogen, so dass sie mit
den anderen monatlich nachschüssigen Zah-
lungen verrechnet werden dürfen. In den letz-
ten 3 Zeilen werden die Verbesserungen durch
rung am Monatsende abgestellt. Um die An-
fangsinvestitionen in t=0 richtig berücksichti-
gen zu können, werden sie mit Wiedergewin-
nungsfaktoren (vgl. z. B. Varnholt/Hoberg/Ger-
hards/Wilms, S. 88 ff.) auf die Monate verteilt.
Es werden nachschüssige Monatsraten ver-
wendet, weil die Personalkosten üblicherweise
am Monatsende zahlungswirksam werden.
Das bedeutet, dass auch alle anderen Auszah-
lungen auf die Monatsenden bezogen werden
bzw. mit Auf- und Abzinsungen dahin transfor-
miert werden müssen. Es soll somit verglichen
werden, zu welchen monatlichen Einsparun-
gen die 4 beschriebenen Handlungsmöglich-
keiten führen. Für die genannten Maßnahmen
seien die Auszahlungen gemäß Abbildung 3
geschätzt worden.
Da es sich um mehrere ähnliche Maschinen
handeln soll, muss unterschieden werden, ob
Investitionen für alle Maschinen insb. in die
Konstruktion getätigt werden (Zeile 1 in Abbil-
dung 3) oder ob es sich um Umbauten/Erweite-
rungen an jeder Maschine handelt (Zeile 3). Zu
den Teilen kommt dann noch der Zeitaufwand
zum Umbau, Testen und Inbetriebnahme (Zeile
4). In Zeile 5 ist die Gesamtinvestition pro Ma-
schine ausgewiesen. Dieses muss nun in nach-
schüssige Monatsraten umgerechnet werden.
Der dazu notwendige effektive Jahreszinssatz
war in Abbildung 1 mit 10% angenommen wor-
inkl. Zinsen entsprechend verteilt werden
müssen. Es seien nun die vier Beispielsstrate-
gien kurz beschrieben:
·
·
Für eine Erhöhung der Taktrate um 10% sei
angenommen, dass dadurch die Efficiency
um 0,5 Prozentpunkte fällt (Zeile 3) und dass
eine halbe Person zusätzlich in der Qualitäts-
kontrolle arbeiten muss (Zeile 11).
·
·
Die Strategie zur Personalreduktion führt zu
einer deutlichen Reduktion der Personalkos-
ten pro Maschinenstunde, aber auch zu einer
leicht verschlechterten Efficiency.
·
·
Im Ansatz zur Efficiencyverbesserung wird
angenommen, dass die Maßnahmen zu einer
Verbesserung um 3 Prozentpunkte (PP) auf
83% führen. Die technischen Maßnahmen
erfordern allerdings auch einen halben Tech-
niker mehr.
·
·
Die Strategie zur Verringerung des Aus-
schusses bringt gleichzeitig eine leicht bes-
sere Efficiency.
Die vier beschrieben Strategien müssen nun
bewertet werden. Dazu ist als erstes zu klären,
wie gemessen werden soll. Man könnte aus der
Investitionsrechnung Kapitalwerte und Endwer-
te einsetzen (vgl. zu diesen Kriterien Varnholt/
Hoberg/Gerhards/Wilms, S. 49 ff.), was sich
aber nicht immer empfiehlt, weil diese Konzep-
te in der Produktion nicht so leicht greifbar sind.
Daher wird auf die monatliche Kosteneinspa-
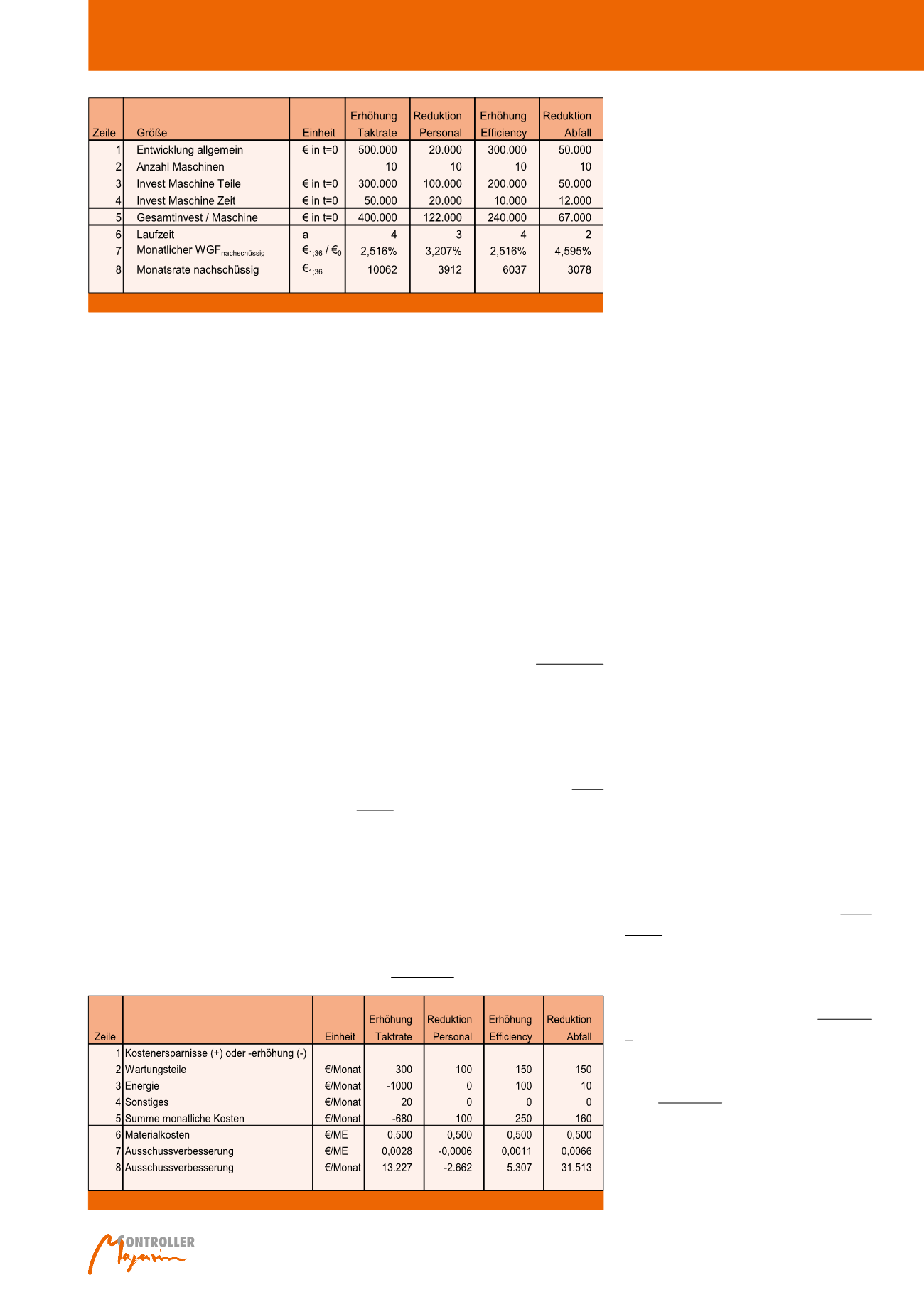
Abb. 3: Notwendige Investitionen und Umrechnung in Monatsraten
Abb. 4: Weitere Einsparungen bzw. Kostensteigerungen
Kostensenkungsstrategien in der Fertigung


