70
wertbildung aller Simulationen mit hinreich-
ender Genauigkeit der Erwartungswert des
Sachverhaltes bei ausreichender Simulations-
anzahl ermittelt werden.
Exkurs 2
Es ist wichtig an dieser Stelle darauf hinzu-
weisen, dass der Erwartungswert bei un-
symmetrischen (schiefen) Dichteverteilun-
gen nicht dem Maximum der Wahrschein-
lichkeitsdichtefunktion entspricht. In unse-
rem Fall liegt er rechts von dem Maximum,
da es sich um eine sogenannte linkssteile
oder rechtsschiefe Verteilung handelt. Das
Maximum selbst wird als Modalwert oder
Modus bezeichnet. Bei symmetrischen Ver-
teilungen – Paradebeispiel Normalverteilung
– sind beide Größen (Erwartungswert und
Modalwert) gleich.
Konkreter Nutzen des skizzierten
Vorgehens
Welcher konkrete Nutzen entsteht durch das
skizzierte Vorgehen oder welche Ergebnisse
sind für das gewählte Beispiel ableitbar?
Grundsätzlich wurde gezeigt, dass sich für der-
artige Sachverhalte keine Wahrscheinlichkeiten
über willkürliche Schätzungen bestimmen las-
sen. Im Beispiel wird erkennbar, wie mit der
Abbildung von derartigen Sachverhalten auch
bei wenigen Eingangsinformationen eine sinn-
volle Darstellung entstehen kann.
der Zusammenfassung der Ergebnisse für die-
ses Beispiel soll noch eine bisher nicht beant-
wortete Frage erörtert werden. Diese lautet:
„Was ist eine Monte-Carlo-Simulation
10
und
wofür wird diese benötigt?“
Monte-Carlo-Simulation: Was und wofür?
Die parametrierte Weibullfunktion in Abbil-
dung 3 war über den Gedanken eines nicht
idealen Vielflächenkörpers entstanden. Da ein
solcher Vielflächenkörper in der Realität un-
möglich herstellbar ist, wird die parametrierte
Funktion zum „Würfeln“ benutzt. Setzt dies
der Rechner mit einer praktisch ausreichend
hohen Anzahl (einige tausend Würfe) um,
spricht man von einer Monte-Carlo-Simulati-
on. Diese entstandenen Simulationen stellen
dann realistische mögliche Ausprägungen des
Problems in der „gewürfelten“ Anzahl dar.
Würden die entstandenen Ergebnisse aufstei-
gend sortiert und kumuliert, entstünde die
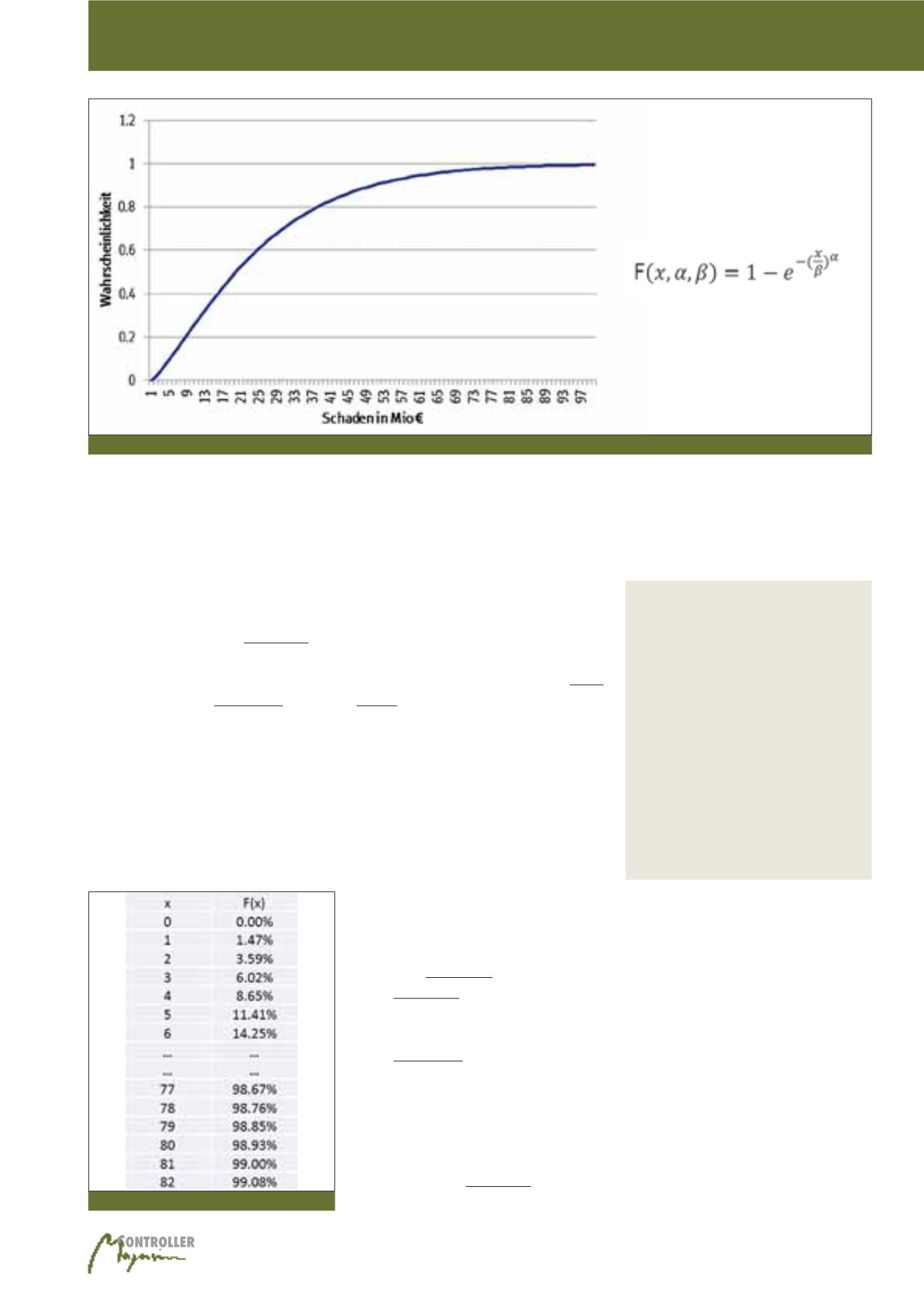
Sicht in der Abbildung 8. Für unser Problem
ist die Abbildung 8 entweder über die gerade
beschriebene Vorgehensweise auf Basis der
Monte-Carlo-Simulation erzeugbar oder über
die in Abbildung 7 gezeigte Funktion bere-
chenbar. Für komplexere Probleme mit meh-
reren Einflussgrößen existiert unter Umstän-
den keine Funktion oder diese ist nur mit er-
heblichem Aufwand erstellbar. Dann bleibt die
Monte-Carlo-Simulation als praktischer Weg
zur Erstellung der in Abbildung 8 gezeigten In-
formationen. Zusätzlich kann über die Mittel-
wahrscheinliche Entstehungsgeschichte des
VaR nachvollzogen worden. Die Unmöglichkeit
der Angabe einer Wahrscheinlichkeit zu einem
Einzelwert, verbunden mit dem Zwang, eine
Wahrscheinlichkeit zu einem Wert angeben zu
wollen, führt genau zu der Sichtweise, die in
der Verteilungsfunktion und damit den Ergeb-
nissen in der nachfolgenden Abbildung 8 zum
Ausdruck kommt.
Beispielhaft kann der Abbildung 8 entnom-
men werden, dass der Schaden mit einer
Wahrscheinlichkeit von 8,65% nicht größer
als 4Mio. € ist, der Schaden mit einer Wahr-
scheinlichkeit von 14,25% nicht größer als
6Mio. € ist, usw ...
Damit ist zunächst geklärt, wie Schäden und
Wahrscheinlichkeiten zusammengehören. Vor
Abb. 7: Verteilungsfunktion
Abb. 8: Tabelle zur Schadenswahrscheinlichkeit
Quantifizierung von schwankungsbehafteten Sachverhalten im RM


