68
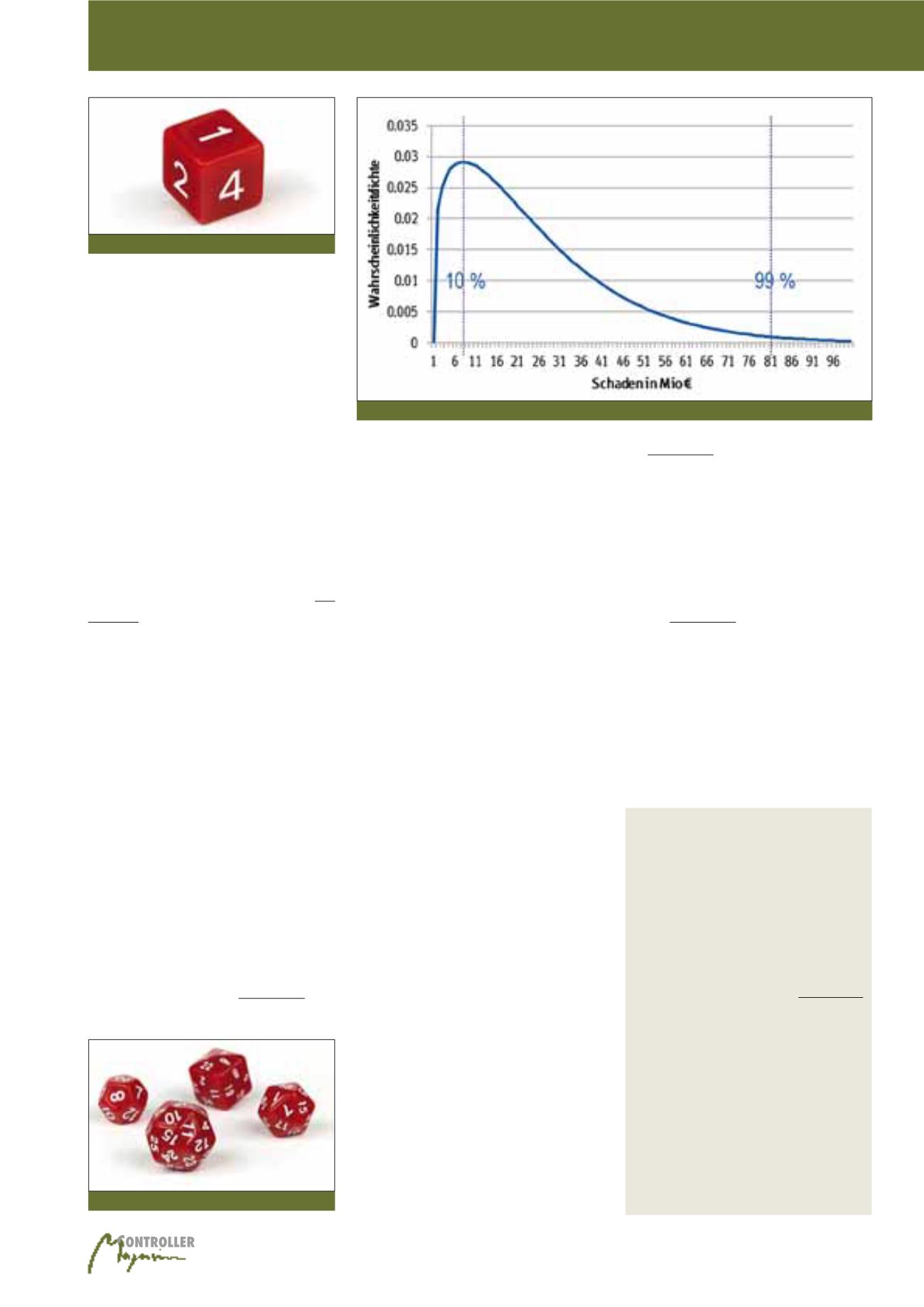
Zur Abbildung 3 unseres Beispiels wird unter
Verwendung der drei bekannten Stützstellen
(Schaden minimal null, realistischer Maximal-
schaden 81Mio. € und häufigste Schäden im
Bereich 10% vom Maximalschaden) eine Funk-
tion angepasst, die in der Grafik dargestellt ist.
Der beispielhafte Maximalschaden von 81Mio. €
ist in der Abbildung 3 mit 99% gekennzeichnet.
Praktisch wird damit zum Ausdruck gebracht,
dass auch die Ermittlung dieses Schadens
einem Irrtum unterliegen kann und mit einer
geringen Wahrscheinlichkeit (1%) die Möglich-
keit noch höherer Schäden besteht. Auf die
korrekte mathematische Interpretation dieser
Wahrscheinlichkeitsaussage wird zu einem
späteren Zeitpunkt noch eingegangen.
Exkurs 1
Für die Leser, deren Interesse über das Ver-
stehen des grundsätzlichen Zusammen-
hangs hinausgeht, sei erläutert, dass für die
Abbildung im Beispiel eine Weibull-Vertei-
lung eingesetzt wurde. Diese Verteilungs-
form führt zu Unrecht immer noch ein Schat-
tendasein, obwohl sie an sehr viele Pro-
bleme sehr gut anpassbar ist. Abbildung 4
zeigt drei wesentliche Möglichkeiten und die
Beschreibung des funktionalen Zusammen-
hangs.
6, 7
Der Formparameter
Į
bestimmt dabei das
Aussehen der Verteilung und der Parameter
ȕ
die Breite. Mit zunehmenden
ȕ
verändert
sich die Lage des Maximums der Dichte-
funktion. Bei einem
Į
gleich 1 ergibt sich
eine weitere Verteilung – die Exponentialver-
teilung – als Grenzfall. Symmetrische Sach-
Die Eintrittswahrscheinlichkeit für die einzelne
Fläche ergibt sich nach wie vor durch P(A)=1/
(Anzahl der Flächen). Bei eins geteilt durch 81
Mio. ist die Wahrscheinlichkeit jedoch fast null.
Damit wird verständlich, dass die Eintrittswahr-
scheinlichkeit des Einzelereignisses mit Zunah-
me der Möglichkeiten gegen null geht.
Löst man nun noch die Idealitätsbedingung auf
– es wird wahrscheinlicher, dass einige Flächen
bei dem Wurf des Vielflächenkörpers häufiger
auftreten, als andere – ist die Anpassung an ein
beliebiges Problem möglich. Die Gleichvertei-
lung wird durch eine problemangepasste andere
Verteilungsform ersetzt.
An dieser Stelle wird klar, dass es unsinnig ist,
in derartigen Fällen einen Maximalschaden mit
einer gefühlten Eintrittswahrscheinlichkeit zu
multiplizieren. Die entstehende Größe entzieht
sich schlicht einer Interpretierbarkeit, da eine
solche Eintrittswahrscheinlichkeit eben nicht
definiert werden kann. Auch extreme Szenari-
en, die zur Beurteilung einer „bestandsgefähr-
denden Entwicklung“
3
nötig sind, werden hier-
von nicht mehr erfasst. Zu allem Überfluß ist
des öfteren zu hören, dies sei doch „prak-
tisch“. Hier bleibt regelmäßig offen, inwiefern
etwas praktisch sein kann, was in der Praxis
nicht vorhanden ist und theoretisch verworfen
werden muss. Auch die oft beworbene „Ein-
fachheit“ eines solch fraglichen Ansatzes er-
schließt sich bei näherer Betrachtung nicht.
Vielmehr erscheint es hoch kompliziert, die
Eintrittswahrscheinlichkeit eines Einzelereig-
nisses zu schätzen, die nicht wesentlich ver-
schieden von null ist.
tretende Schaden könnte die Werte 1 €, 2 €,
..., 100.000 €, ... 81 Mio. € oder alle Werte
dazwischen annehmen. Über den Umstand,
dass theoretisch unendlich viele Nachkom-
mastellen möglich sind, ist an dieser Stelle
schon klar, dass es unendlich viele Möglich-
keiten gibt. Die Wahrscheinlichkeitsdichte-
funktion ist dann stetig.
Da die in der Realität eintretenden Schäden in
hohem Maße vom Zufall geprägt sind, kann
der Würfel als Sinnbild hierfür verstanden wer-
den. Mit Blick auf einen (idealen) Würfel wird
sich der Leser erinnern, dass die Eintritts-
wahrscheinlichkeit P(A) sich durch 1/(Anzahl
der Flächen) ausdrückt. Beim Würfel (vgl. Ab-
bildung 1) ergibt sich also für die einzelne Flä-
che P(A)=1/6. Ideal meint dabei die Annahme,
dass alle Flächen gleichwahrscheinlich sind.
Über eine hohe Anzahl von Würfen würde sich
etwa eine Gleichverteilung der einzelnen Zah-
len ergeben.
Gäbe es in der Realität nur sechs Möglichkei-
ten, wäre ein Würfel ausreichend. Jeder Seite
wäre eine der Möglichkeiten zuordenbar.
Ein „Würfel“ mit 81 Millionen Flächen
Da das beschriebene Beispiel 81 Mio. Möglich-
keiten kennt – auf die Betrachtung der Nach-
kommastellen wird hier verzichtet –, genügt der
Würfel nicht mehr. Er wird zum Vielflächenkör-
per mit 81 Mio. Flächen – Abbildung 2 stellt
solche in unterschiedlichen Ausprägungen dar.
Abb. 1: Die Würfel-Analogie
Abb. 2: Vom Würfel zum Vielflächenkörper
Abb. 3: Funktion der Schadenswahrscheinlichkeit
Quantifizierung von schwankungsbehafteten Sachverhalten im RM


