69
Hieraus wird ersichtlich, dass die Klasse mit
dem theoretischen Maximalschaden bei einer
Klassenbreite von 5 Mio. € gerade einmal
0,33% der Werte beinhaltet. Einmal mehr wird
deutlich, dass ein willkürliches Schätzen von
Eintrittswahrscheilichkeiten nicht einmal bei der
Verwendung von Intervallwahrscheinlichkeiten
zu im Risikomanagement verwendbaren Ergeb-
nissen führt. Verwendbar hingegen ist die kumu-
lierte Form der Dichtefunktion – die Verteilungs-
funktion (vgl. Abbildung 7).
Analogie zum im Bankensektor
verwendeten Value-at-Risk
Aus Verteilungsfunktionen gewinnt man eine
Aussage, die tatsächlich aufgrund des kumula-
tiven Gedankens mit einer Wahrscheinlichkeit
verknüpfbar ist. Die Aussage lautet dann: „Mit
einer Wahrscheinlichkeit von y% (in der Abbil-
dung 8 aus F(x) resultierend) ist der Schaden
nicht größer als x €.“ Inhaltlich entspricht dies
dem Gedanken des im Bankensektor schon
länger verwendeten VaR (Value-at-Risk). Der
VaR stellt ein so genanntes Risikomaß dar. Risi-
komaße werden in unterschiedlicher Ausprä-
gung verwendet. Weiterführend sei auf Fußnote
8
und
9
verwiesen. Ergänzend ist auszuführen,
dass ein weiteres Risikomaß in ähnlicher Ver-
wendung, der CVaR (Conditional Value-at-Risk),
existiert. Auch hierfür ist die erklärte Vorge-
hensweise als Basis anzusehen.
Damit sind nicht nur fast alle eingangs formu-
lierten Fragen beantwortet, sondern auch die
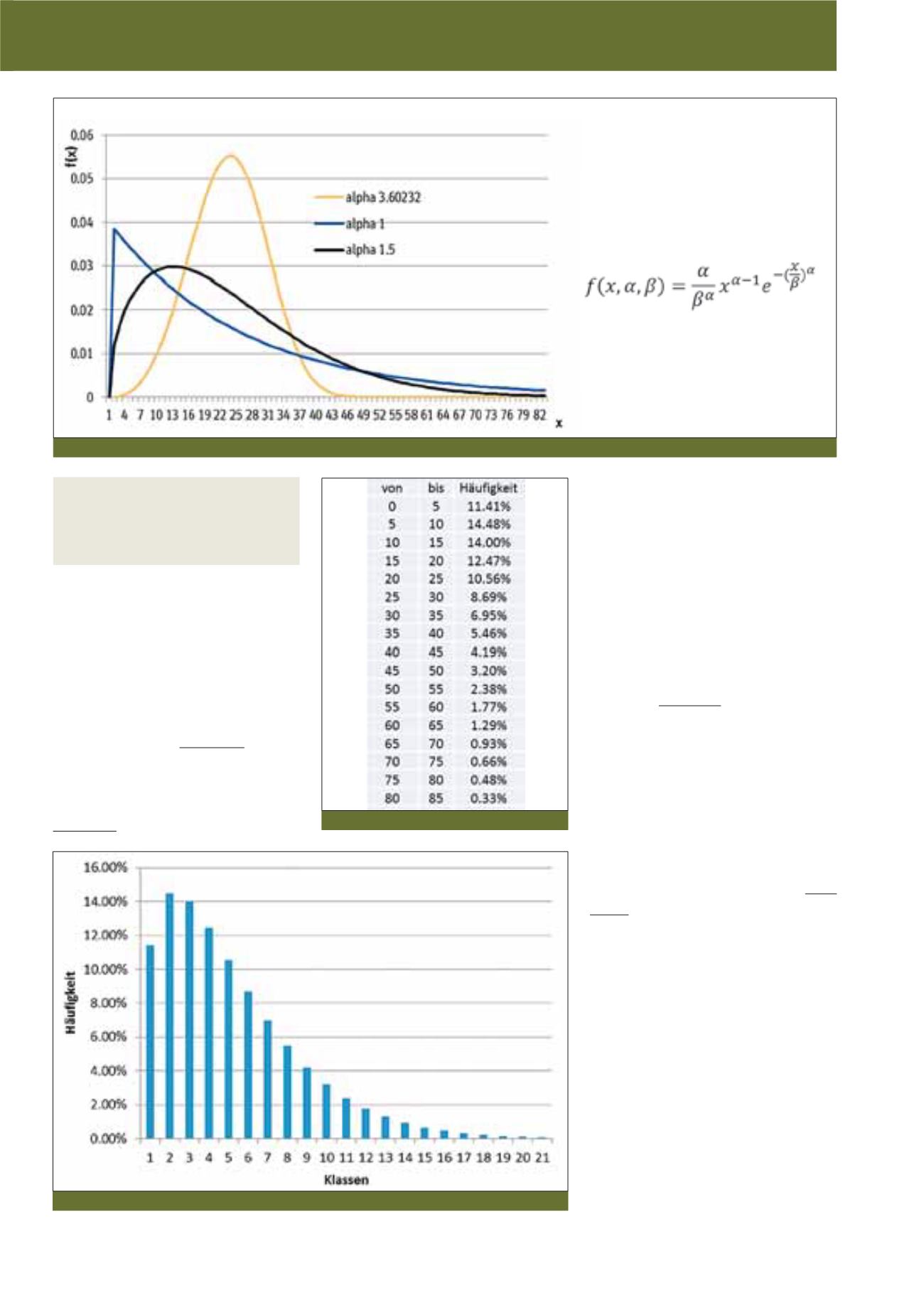
verhalte – diese werden häufig durch die
Normalverteilung abgebildet – sind ebenfalls
durch eine Weibullverteilung (
Į
=3,60232)
beschreibbar.
Bisher noch nicht erklärt, aber ebenfalls von
grundsätzlicher Bedeutung ist die Aussage zum
dritten Punkt – also die Aussage zu
Intervall-
wahrscheinlichkeiten
. Diese lassen sich na-
türlich auch dann angeben, wenn einzelne
Punkte keine wesentlich von null verschiede-
nen Eintrittswahrscheinlichkeiten haben. Für
das Beispiel würde die Abbildung 5 von Inter-
vallwahrscheinlichkeiten in Form einer Häufig-
keitsverteilung ein signifikantes Bild ergeben.
Tabelliert man die Werte, so ergibt sich die in
Abbildung 6 dargestellte Sicht
Abb. 4: Zweiparametrische Weibullverteilung – Dichteverteilung
Abb. 5: Häufigkeit von Intervallwahrscheinlichkeiten
Abb. 6: Tabelle der Häufigkeitsverteilung
CM März / April 2018


