33
schien. Sobald Unternehmen eine Planabwei-
chung erkennen, die nicht im Vorfeld durch
das Risikomanagement bestimmt wurde, ist
damit ein neues Risiko identifiziert. In diesem
Zusammenhang lässt sich durch eine syste-
matische (längerfristige) Abweichungsanalyse
eine Datengrundlage über tatsächliche Plan-
abweichungen erzeugen. Auf Basis dieser Da-
ten kann das Unternehmen Risiken quantifi-
zieren und mithilfe statistischer Verfahren die
nötige Verteilung berechnen.
Erwartungswert als Planwert
Das Unternehmen verfügt nun über den gefor-
derten Erwartungswert sowie über die Band-
breiten der Planwerte (wie bspw. von den GoP
empfohlen). Auch kann mit diesem Verfahren,
wie im IDW PS 340 gefordert, das Unterneh-
men eine verlässliche Risikoaggregation ge-
währleisten. Der Erwartungswert kann somit
als neuer Planwert aufgenommen werden.
30
Denn dieser Wert beinhaltet die verschiedens-
ten Risikokonstellationen und sollte sich im
„Mittel“ aus vielen potenziellen Planszenarien
als richtig herausstellen. Infolgedessen sind
die Risiken adäquat in die Planung übertragen
sowie berücksichtigt und die Unsicherheit mit
der Bandbreite visualisiert. Obendrein verbin-
det sich das Risikomanagement mit der Pla-
nung, und beide Funktionen tragen ihren An-
teil zu einer gemeinsamen – realitätsnäheren
– Planung bei. Ergänzend auf diesen „neuen“
Planwerten können dann auch zwischen Con-
trolling und Risikomanagement gemeinsame
Kennzahlen entwickelt werden. Dies ermög-
licht, in komprimierter Form regelmäßig Ab-
weichungen zu kommunizieren und Steue-
rungsimpulse zu geben.
31
narien anstatt weniger Kombinationen erleich-
tert die Simulation einerseits die Arbeit des Pla-
ners, anderseits bildet sie eine realitätsnähere
Entwicklung ab.
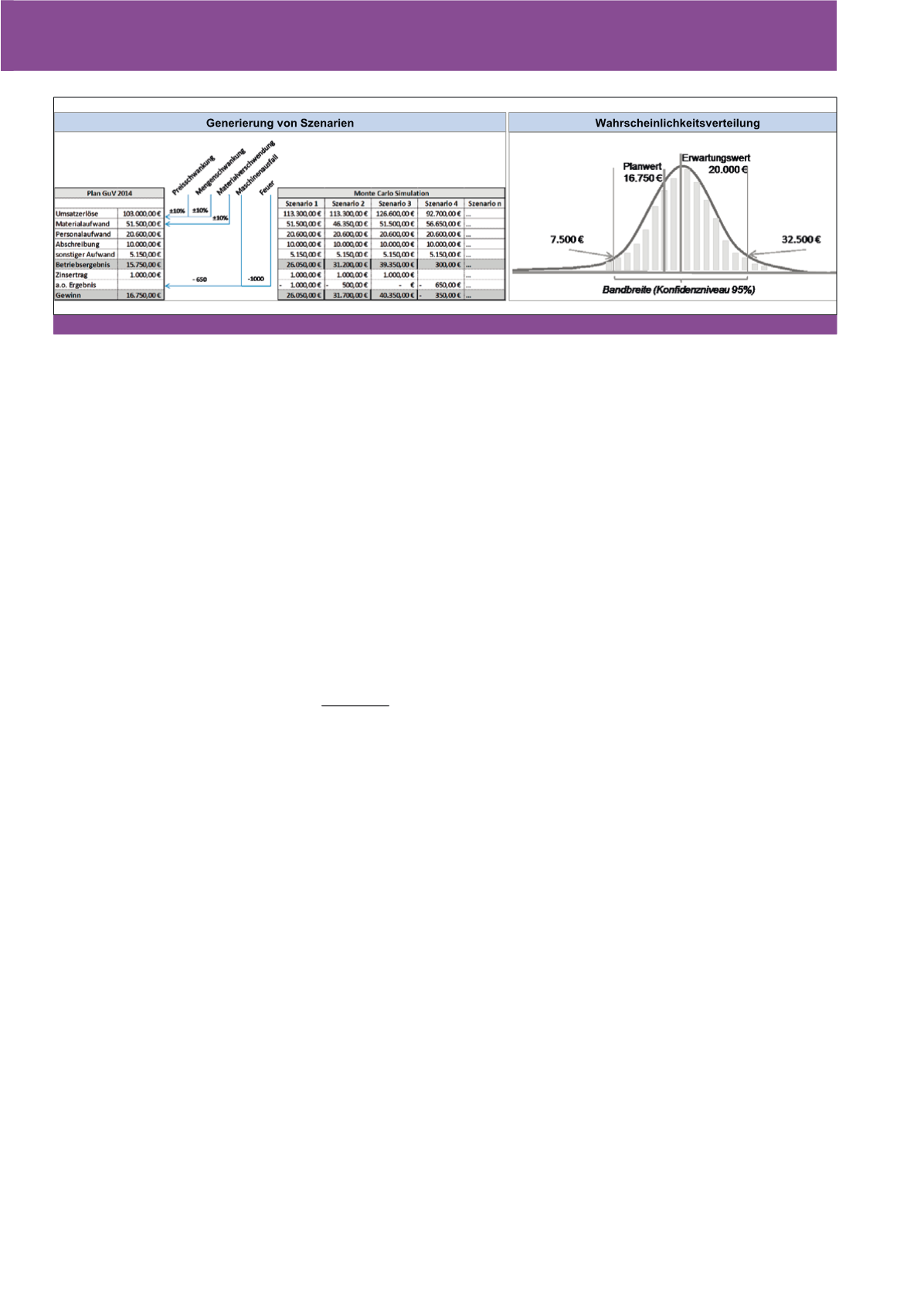
Ergebnis
Für die jeweiligen Planpositionen ergeben
sich aus der repräsentativen Stichprobe sta-
bile Verteilungen, aus denen der Planer den
Erwartungswert und die Schwankungsbreite
ableitet.
27
In Verbindung mit einem Konfi-
denzniveau
28
lässt sich die gewünschte Band-
breite bestimmen, dies veranschaulicht zu-
gleich das Sicherheitsniveau der Planung (vgl.
Abbildung 3). Also mit welcher Wahrschein-
lichkeit der potenzielle Ist-Wert zwischen ei-
nem oberen und unteren Wert liegt bzw. die
Werte nicht über-/unterschritten werden.
Überträgt man dies auf die Abbildung, so er-
rechnet sich aus dem ursprünglichen Plan-
wert (16.750 €) und den Risiken ein Erwar-
tungswert des Gewinns von 20.000 €, wel-
cher zu 95% nicht geringer als 7.500 € und
nicht höher als 32.500 € ausfällt.
Abweichungsanalyse
Nach Ende der Planungsperiode kann mittels
einer Abweichungsanalyse eine Risikoidentifi-
kation und -quantifizierung erfolgen. Da das
Unternehmen zur Planung schon Kenntnis
über mögliche Planabweichungen hatte, ist
nicht jede Planabweichung eine „tatsächliche“
Abweichung. Controller/Risikomanager müs-
sen vielmehr analysieren, ob man im Vorfeld
über diese mögliche Planabweichung infor-
miert war und ob der Umfang passend er-
bedarf es für eine konsequente Risikoquantifi-
zierung einer ordentlichen Datenqualität (die die
Kriterien für eine statistische Auswertung er-
füllt), welche ebenso die Planungssicherheit er-
höht. Bei mangelnder Datenqualität kann eine
passende
23
Schätzung durchgeführt werden.
Diese kann zu Beginn vorsichtig, also breiter
aufgestellt werden.
24
Allerdings wird sich im
Laufe der Zeit die Datenqualität resp. Schät-
zung durch eine kontinuierliche risikoadjustierte
Planung verbessern. Eine Schätzung ist immer
besser, als gar keine Risikoquantifizierung vor-
zunehmen, denn so ist man auch für den Risi-
koeintritt sensibilisiert. Lediglich bei einem
qualitativen Ansatz sind die Risiken zu be-
schreiben und nicht (monetär) zu quantifizieren,
was ebenfalls hilfreicher ist, als gar keine Risi-
koeinschätzung vorzunehmen.
Monte-Carlo-Simulation
25
Die Monte-Carlo-Simulation ist eine Simulation
von möglichen realistischen Szenarien, die auf
diversen zufallsbeeinflussten Ereignissen beru-
hen. Demnach bildet die Simulation eine Viel-
zahl von potenziellen Szenarien mit Hilfe von
„Pseudo-Zufallszahlen“. Je Durchlauf weist sie
jedem (Planungs-) Parameter zufällig, unter Be-
rücksichtigung der Verteilung – die jeweilige Ri-
sikoquantifizierung – einen neuen Wert zu und
speichert das Ergebnis. Jeder Durchlauf gene-
riert somit ein eigenständiges Szenario. Somit
aggregiert die Simulation diverse Risikokombi-
nationen und bildet eine Wahrscheinlichkeits-
verteilung darüber.
26
Bis eine repräsentative
Stichprobe besteht, benötigt es je nach Kom-
plexität der Planung mehrere tausend Durch-
läufe, wenn nicht sogar bis zu einer Million.
Aufgrund der Generierung von unzähligen Sze-
CM November / Dezember 2018
Abb. 3: Vom Planwert zum Erwartungswert
29


