27
weil die Kosten von Periode zu Periode unter-
schiedlich sein können.
Wenn die Gesamtkosten von 300 €/Pe durch
die Periodenmenge dividiert werden, erhält man
den totalen Stückkostensatz zu 300 €/Pe / 10
ME/Pe = 30 €/ME (siehe erste Zeile für Maschi-
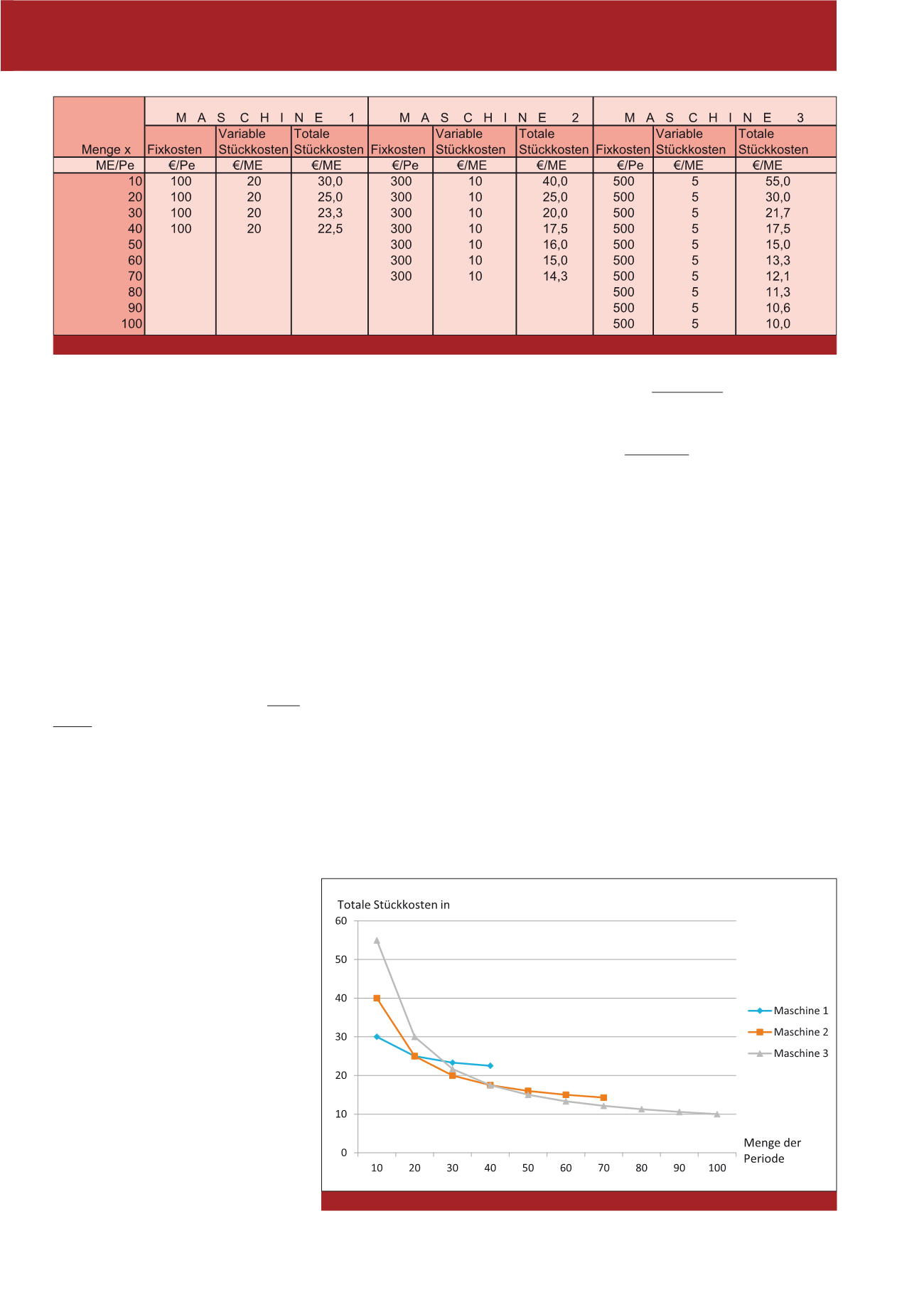
ne 1). Mit steigender Menge sinken die totalen
Stückkosten, bis sie bei der Maximalmenge von
40 ME/Pe ihr Minimum von 22,5 €/ME erreichen.
Deutlich höhere Fixkosten sind bei Maschine 2
zu tragen, die dafür aber auch nur die halben
variablen Stückkosten erfordert. Bei einer Men-
ge von nur 10 ME/Pe weist sie mit 40 €/ME zu-
nächst höhere Stückkosten auf (siehe Abbil-
dung 1). Aber schon bei 20 ME/Pe wird das
gleiche Kostenniveau erreicht (Break-even) und
bei Maximalmenge ist sie mit 14,3 €/ME deut-
lich günstiger. Ihre Leistungsgrenze erreicht sie
bei einer Periodenmenge von 70 ME/Pe.
Die dritte Maschine bringt eine noch höhere
Leistung und erzeugt daher hohe Fixkosten,
aber geringe variable Stückkosten. Bei ihrer
Maximalmenge von 100 ME/Pe hat sie mit 10
€/ME die geringsten Stückkosten. Unter sonst
gleichen Bedingungen und hinreichender Nach-
frage würde das Unternehmen mit Maschine 3
am günstigsten fahren.
Die Daten sind so gewählt, dass die üblichen
Ergebnisse resultieren. Kleine halbautomati-
sche Maschinen sind geeignet für geringe
Mengen; bei mittleren Mengen macht eine au-
tomatische Maschine Sinn und bei sehr hohen
Mengen eine Hochleistungsmaschine.
Interes-
sant sind die Grenzmengen (Break-even-
Mengen)
, von denen an die jeweils größere
Maschine vorteilhaft wird. Sie werden ermittelt,
indem die Differenz der Fixkosten durch die Dif-
ferenz der variablen Stückkosten dividiert wird:
BEM
1vs2
= (K
fix2
– K
fix1
) / (k
v1
-k
v2
)
in €/Pe / €/ME = ME/Pe
BEM1
vs2
Break-even-Menge der Maschinen
1 und 2 in ME/Pe
K
fix1
Periodenfixkosten der Maschine
1 in €/Pe
k
v1
Variable Stückkosten der Maschine
1 in €/ME
Im gezeigten Beispiel beträgt die Break-even-
Menge für die Vorteilhaftigkeit der Maschine 1
vs. Maschine 2 (300-100) / (20-10) = 20 ME/
Pe. Bei dieser Menge weisen beide Maschinen
totale Stückkosten von je 25 €/ME auf. Dieses
Ergebnis lässt sich auch aus der obigen Abbil-
dung entnehmen. Bei (500-300) / (10-5) = 40
ME/Pe erzeugen Maschine 2 und 3 die glei-
chen totalen Stückkosten von 17,5 €/ME. In der
folgenden Abbildung 2 sind die jeweiligen
Schnittpunkte einfach abzulesen.
In der Abbildung 2 sind die Verbindungen zwi-
schen 2 Punkten der Einfachheit halber mit Ge-
raden dargestellt. Genauer wäre eine Verbin-
dung, die erst stärker und dann schwächer fällt
(konvexer Verlauf). Bei der Analyse der Kosten-
funktionen ist die Erkenntnis wichtig,
dass sol-
che Kostenfunktionen immer nur für die
betrachtete Periode gelten
. Zudem ist es
außerordentlich kompliziert, die Fixkosten
aufgrund von Investitionen am Anfang oder
Entsorgungskosten am Ende der Laufzeit auf
die jeweiligen Perioden zu verteilen (vgl. zu
den möglichen Problemen in der Break-even-
Rechnung Hoberg (2014a), S. 759 ff.).
Im nächsten Schritt sei die Gesamtstückkos-
tenfunktion über alle Maschinen abgeleitet. In
der VWL wird diese Funktion die umhüllende
genannt. Sie besteht aus den Kostenminima
der Funktionen der einzelnen Maschinen, wie
Abb. 1: Beispiel: Totale Stückkosten für 3 Maschinen
Abb. 2: Verlauf der totalen Stückkosten bei 3 Maschinen
CM September / Oktober 2017


