82
sich an den echten Erwartungen des Unter-
nehmens. Diese Herangehensweise ergänzt
die Szenarioanalyse durch das Aggregieren
der Auswirkungen unterschiedlicher Entwick-
lungen. Außerdem entsteht eine realistische
Betrachtungsweise der Quantifizierung von
Eintrittswahrscheinlichkeiten, sowie der Er-
wartung bezüglich der Best- und Worst-Case-
Szenarien. Der Controller bekommt Abwei-
chungen vom Erwartungswert und der Wahr-
scheinlichkeit des Eintritts einzelner Szenarien
gemäß seiner eingespeisten Verteilungsfunkti-
onen (Input-Erwartungen) bewertet.
Limitationen
Es wurde bereits erwähnt, dass die verwende-
ten Wahrscheinlichkeitsfunktionen als Input der
Simulation mit dem Fehler der Erhebung behaf-
tet sind. Oftmals liegen nicht genügend Daten
vor, um eine Verteilungsfunktion zu identifizie-
ren, sodass es notwendig ist, eine Annahme zu
treffen. Außerdem kann nicht davon ausgegan-
tungshaltung an verschiedene Einheiten des
Unternehmens entsteht. Betrachtet man nur
eine Business Unit, so kann man im Rahmen
der Planungserwartungen ebenfalls eine Ab-
weichung feststellen, die sich allerdings bei der
Erweiterung der Anschauungsperspektive auf
mehrere unterschiedliche Business Units ver-
größert. Anders verhält es sich mit dem Erwar-
tungswert. Dieser ist die kombinierte Erwar-
tung aller Bereiche.
Benefit
Mit der Anwendung der Monte-Carlo-Methode
werden die empirisch feststellbare Unsicher-
heit der Planung in der Vergangenheit sowie
externe Einflussfaktoren in die Zukunft extra-
poliert. Sinnvoll ist die Anwendung vor allem,
wenn die Entwicklung verschiedener Bereiche
aggregiert betrachtet werden soll. Unsicher-
heit wird im Rahmen der empirisch feststellba-
ren Abweichungen der Vergangenheit im Mo-
dell inkorporiert. Erwartungswerte orientieren
mulationsperiode (= 1 Jahr) simuliert, sondern
aufbauend auf den Ergebnissen weitere Simu-
lationen berechnet. Hierbei entstehen im Rah-
men der Simulation n-Pfade, die anhand der
vorher definierten Input-Wahrscheinlichkeits-
verteilungen zufällig errechnet werden. Diese
werden als einzelne Szenarien aufgefasst.
Die Entwicklung im dargestellten Fall ist positiv
ausgefallen. Dies liegt an den zugrundeliegen-
den Wachstumserwartungen. Während zwei
der drei Business Units rückläufiges Wachstum
erwarten, sind die Wachstumserwartungen der
dritten Business Unit vielversprechend, sodass
das rückläufige Geschäft der ersten beiden Ein-
heiten kompensiert wird. Die Monte-Carlo-Me-
thode eignet sich insbesondere, wenn verschie-
dene Bereiche und deren gemeinsame Ent-
wicklung betrachtet werden sollen. Insofern er-
möglicht die Durchführung der stochastischen
Simulation eine Zusammenfassung der kombi-
nierten Wachstumserwartung der verschiede-
nen Bereiche, gibt aber gleichzeitig Aufschluss
über die erhöhte Volatilität, die durch die Erwar-
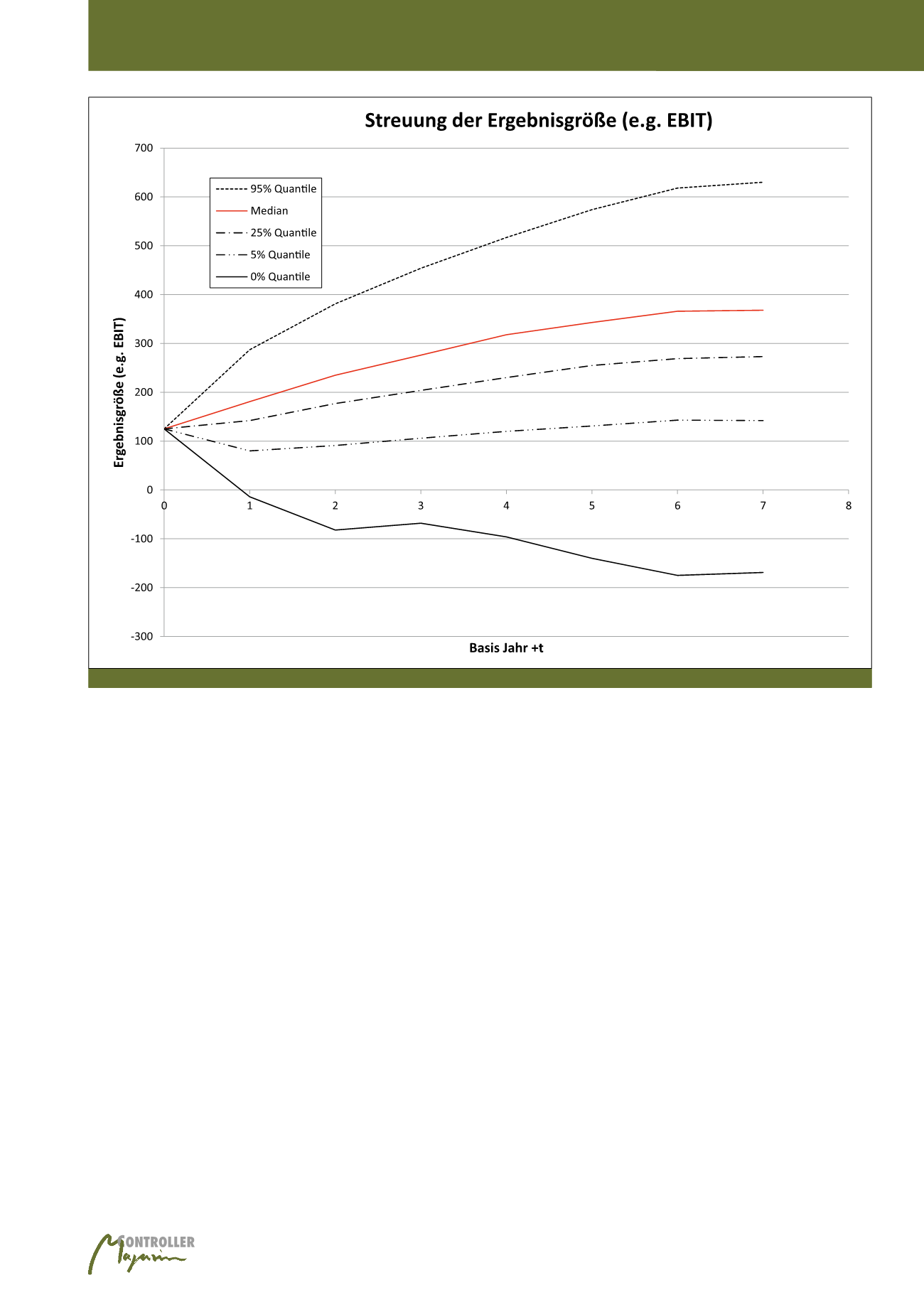
Abb. 5: Querschnitt der Quantil Struktur der Ergebnisse aller Simulationsdurchläufe
Szenario-Analyse durch stochastische Simulation


