81
Auswertung der Ergebnisse
Das Ergebnis ist interpretationsbedürftig und
erlaubt Rückschlüsse auf das ursprüngliche
Problem. Dazu werden die Ergebnisse der Simu
lation in einem Histogramm veranschaulicht.
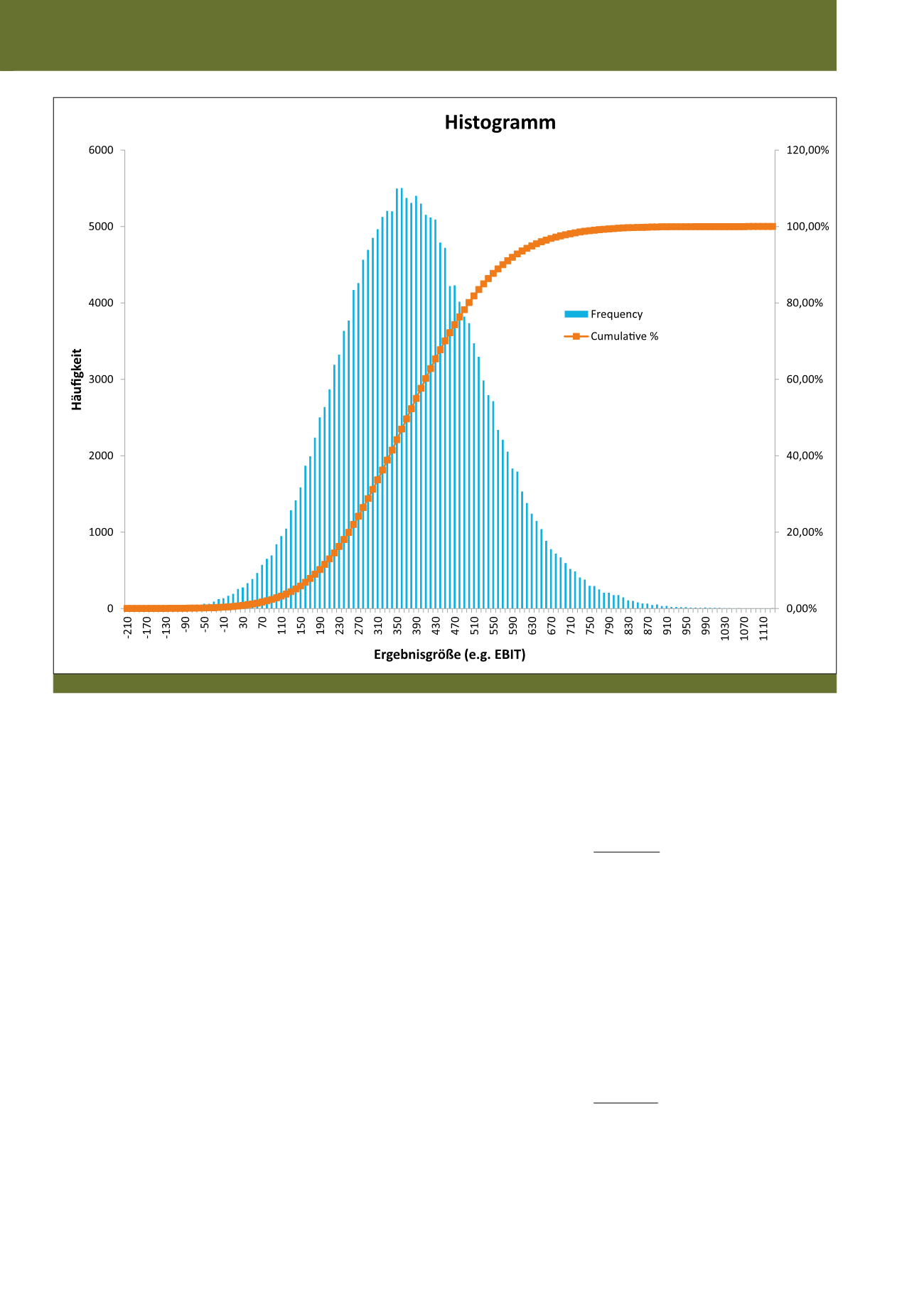
(Abbildung 4 zeigt ein Histogramm, welches die
Häufigkeitsverteilung der Ergebnisse einer Si-
mulation darstellt.)
Aus der Lage der Streuung lässt sich des Wei-
teren eine Wahrscheinlichkeitsdichtefunktion
approximieren. Außerdem kann die Quantil-
Struktur der Ergebnisfunktion festgestellt wer-
den, was Aufschluss über die anfänglichen
Fragestellungen nach dem Best- und Worst-
Case sowie dem Abschätzen der Eintrittswahr-
scheinlichkeiten der einzelnen Outputs gibt.
(Abbildung 5 zeigt die Quantil-Struktur der Er-
gebnisgröße.)
Im Beispielfall wurde eine Simulation für das
EBIT des Unternehmens durchgeführt. Dabei
wurden nicht nur die Ergebnisse der ersten Si-
der letzten Jahre, projiziert man somit einge-
troffene Unsicherheiten der Vergangenheit in
die Zukunft.
Im vierten Schritt
werden die getroffenen An-
nahmen sowie das formale Modell in einem
Si-
mulationsmodell
umgesetzt. Hierfür werden
mithilfe eines Zufallsgenerators unabhängige
und gleichmäßig verteilte Zufallszahlen gene-
riert, die den zuvor definierten Verteilungsfunk-
tionen der Simulationsparameter entsprechen.
Dabei gibt es die Möglichkeit, auf kostenpflich-
tige Add-Ins für Microsoft Excel zurückzugrei-
fen oder unter Inanspruchnahme der eingebet-
teten Excel-Funktionen in VBA selbst einen
Simulationsalgorithmus zu programmieren.
Im fünften und letzten Prozess-Schritt
wird
mit dem erstellten
Simulationsprogramm
die
Simulation durchgeführt. Wichtig ist, dass eine
ausreichende Anzahl von Simulationsdurchläu-
fen berechnet wird. Wie hoch diese Anzahl ist,
hängt von der Standardabweichung der Ergeb-
nisfunktion ab.
Höhe, verglichen mit dem Umsatz, höher von
der Entwicklung der anderen externen Fakto-
ren (Lohnkostenniveau, etc.) abhängen.
Der dritte Schritt
– das
stochastische Mo-
dell
– beinhaltet die Reduktion der zu simulie-
renden Variablen auf stochastische Größen.
So werden sämtliche Simulationsvariablen als
Wahrscheinlichkeitsfunktionen ausgedrückt.
Für diesen Zweck werden deren Lageparame-
ter ermittelt. Eine mögliche Herangehensweise
kann dabei sein, die Erwartungswerte der
Wahrscheinlichkeitsfunktion zum Zweck der
Simulation qualitativ (als Planerwartung), die
Streuungsparameter quantitativ (als histori-
sche Abweichung) zu ermitteln. Wichtig ist,
dass eine ausreichende Menge historischer
Daten vorliegt, um von einer mathematischen
Abhängigkeit in der Analyse historischer Daten
zu sprechen. Dieser Punkt ist in der Praxis oft-
mals problematisch, da wechselnde Unterneh-
mensstrukturen und ERP-Systeme die Aus-
wertung der Daten erschweren. Verwendet
man historische Werte, wie Planabweichungen
Abb. 4: Histogramm der Simulationsergebnisse nach dem letzten Simulationsdurchlauf
CM März / April 2019


