76
– wie im vorangegangenen Beispiel – die be-
reits vorhandenen Daten genutzt, um ein Mo-
dell zu trainieren. Für ein ARIMA-Modell sollte
heuristisch eine Mindestanzahl von 40-50
Beobachtungen (Zeitpunkte) vorliegen, um
eine statistische Zeitreihenanalyse inklusive
Vorhersage durchführen zu können. Von die-
sen Beobachtungen werden 75 Prozent ge-
nutzt, um das dahinterliegende Prognosemo-
dell soweit zu optimieren (Trainingsphase des
Modells), dass es die verbleibenden 25 Pro-
zent möglichst genau vorhersagt (Validie-
rungsphase des Modells). Wenn man bei-
spielsweise auf monatlicher Basis eine Analy-
se durchführen möchte, so sollten drei Jahre
Historie für die Trainingsphase und ein Jahr
Historie für die Validierungsphase eingesetzt
werden. Führt man diese Trainings- und Vali-
dierungsphase für mehrere Modelle durch,
lässt sich anschließend erkennen, welches
Modell die besseren Prognosen liefert.
Der Aufwand, der durch die Modellierung der
Modelle entsteht, wird durch die Genauigkeit
und Flexibilität der finalen Prognosen gerecht-
fertigt. Sobald die Modelle einmal trainiert und
validiert sind, lassen sie sich im späteren Pro-
zess individuell anwenden oder Simulationen
durchführen.
Automatischer Planungsprozess
Wie können diese Erkenntnisse und Modelle in
den Planungsprozess integriert und wie kann
dieser dadurch optimiert werden? Eine Einspa-
rung von 90 Prozent des Aufwands innerhalb
des Planungsprozesses wäre wünschenswert.
Eine solch pauschale Aussage kann jedoch auf-
grund vieler unterschiedlicher Parameter inner-
halb eines Unternehmens und der zu prognosti-
thoden bessere Ergebnisse. Die Güte eines
Modells, welche durch die jeweilige Methode
bedingt wird, hängt immer von der Struktur
der Daten ab. Zwar bedeutet dies immer einen
anfänglichen Mehraufwand, jedoch ist es
sinnvoll, auch mehrere Modelle zu testen und
gegeneinander zu vergleichen. Dafür werden
Ein Nachteil des ARIMA-Ansatzes ist die be-
dingte Funktion. Denn diese Methode erzielt
nur Ergebnisse, wenn Muster in den Daten vor-
handen sind. Zudem benötigt sie relativ viele
historische Daten, und der Aufwand für eine
Modellentwicklung ist deutlich höher. Dem ge-
genüber steht die Qualität der Prognosen, so-
bald der Aufwand einmal betrieben wurde und
die entsprechende Datengrundlage vorliegt
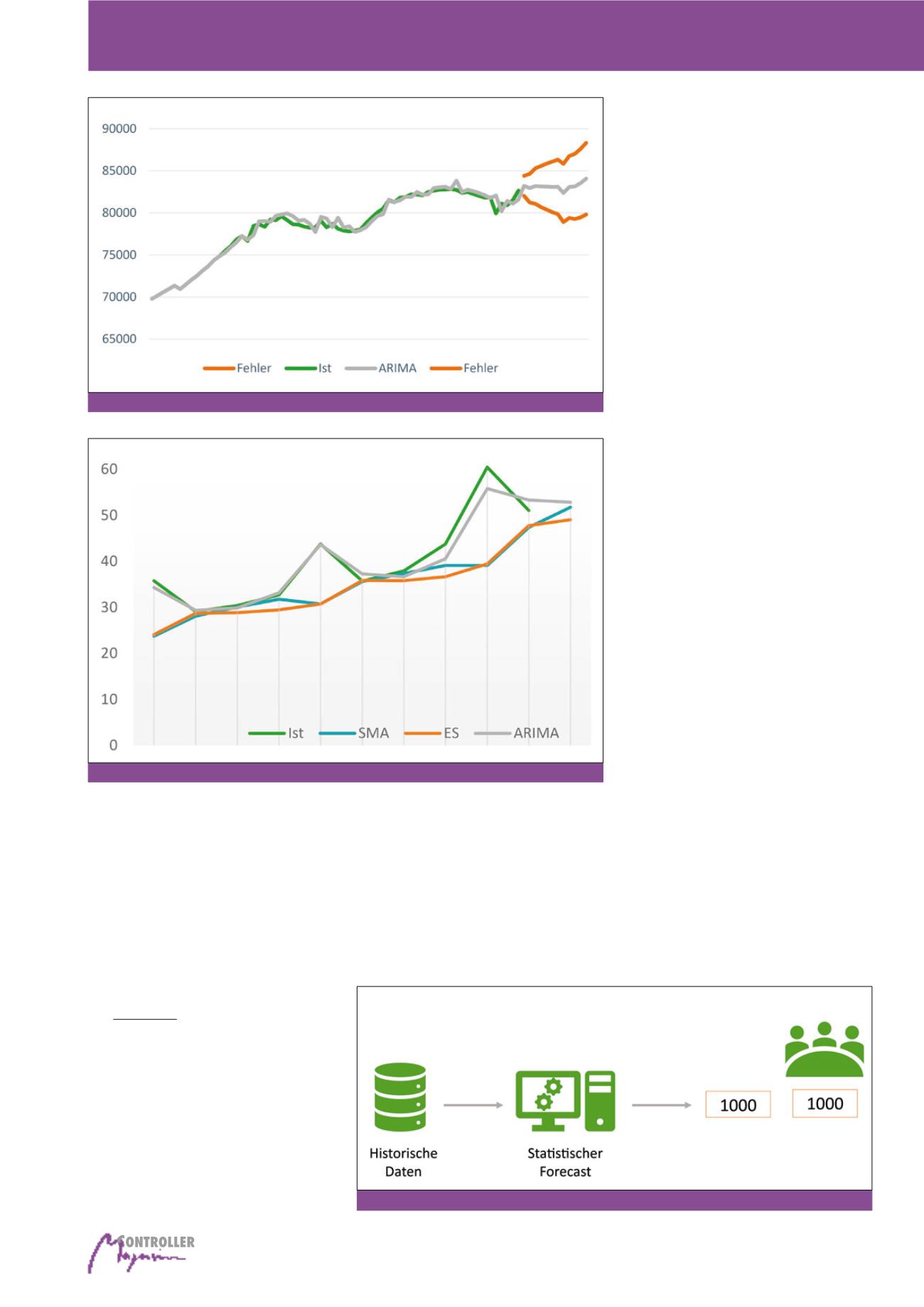
(vgl. Abbildung 8).
Für das hier betrachtete Beispiel kann klar die
Aussage getroffen werden, dass mit der ARI-
MA-Methode bessere Prognosen erreicht
werden. Grundsätzlich lässt sich jedoch keine
pauschale Aussage treffen, wann sich welche
Methode optimal eignet. Auch die Optimalität
der ARIMA-Methode kann nicht garantiert
werden. In einigen Fällen liefern andere Me-
Abb. 9: Automatischer Planungsprozess
Planungsprozesse mit „statistischem Forecast“
Abb. 7: Fehlergrenzen Einwohnerbeispiel
Abb. 8: Detailvergleich


