75
beiden Kurven sind in diesem Fall fast de-
ckungsgleich und somit wären die Vorhersagen
deutlich näher an den tatsächlichen Werten
(vgl. Abbildung 5).
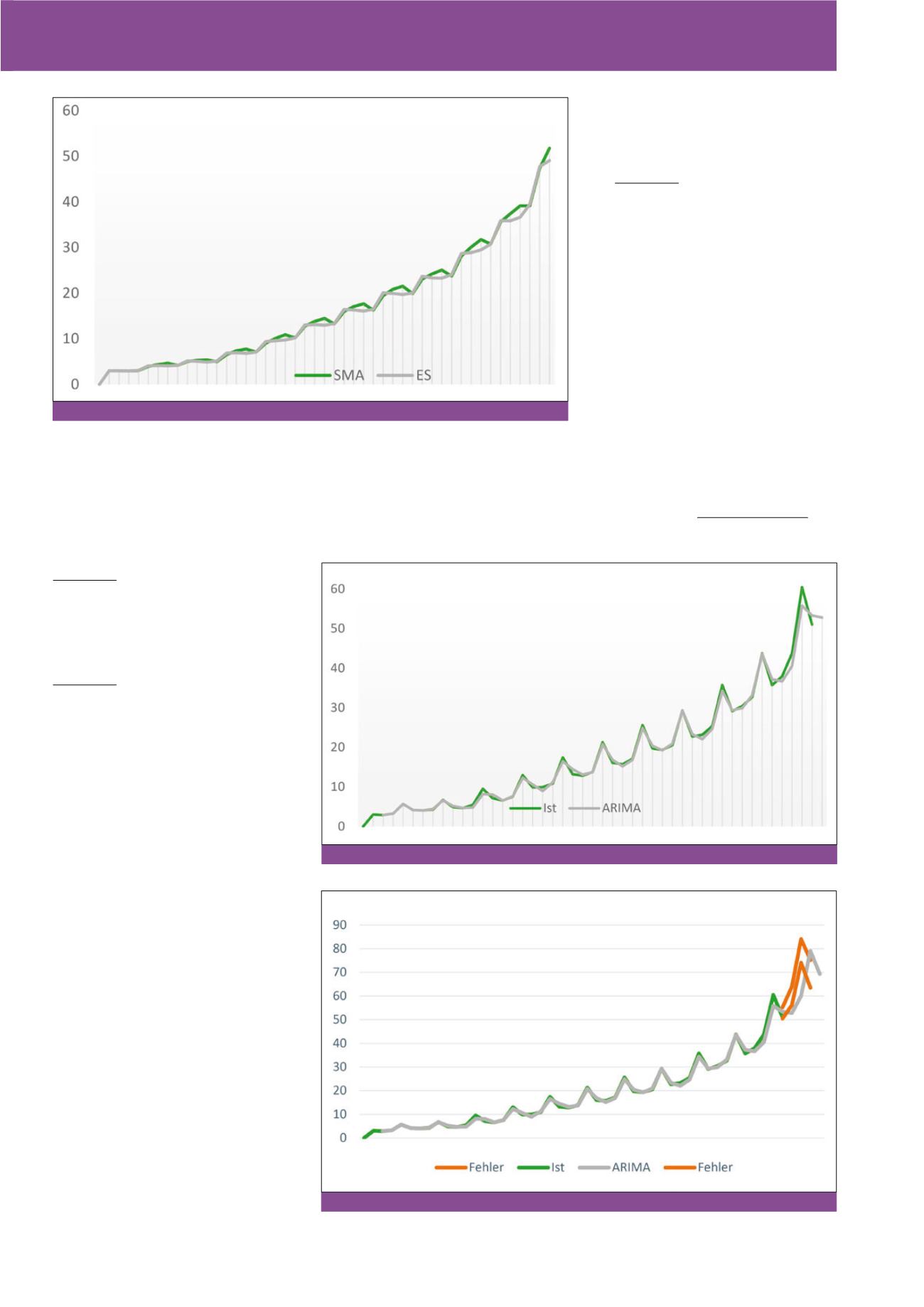
Soll das resultierende ARIMA-Modell zur Vor-
hersage genutzt werden, so kann die Güte der
Vorhersage mit grafischen Mitteln bestimmt
werden. Darüber hinaus liefert die ARIMA-Me-
thode zusätzlich Fehlergrenzen, die der Güte-
vorhersage dienen. Je weiter diese Fehlergren-
zen (Fehler) auseinander liegen, desto stärker
ist die Prognose mit Unsicherheit behaftet. Bei
dem Vergleich zweier unterschiedlicher Zeitrei-
hen (hier das bekannte Umsatz-Beispiel sowie
die Entwicklung der Einwohnerzahl Deutsch-
lands) lässt sich erkennen, je ungleichmäßiger
die Daten sind, desto weiter gehen die Fehler-
grenzen auseinander und die Prognosen wer-
den ungenauer (vgl. Abbildungen 6 und 7).
Auch für ARIMA wird erneut das Umsatz-Bei-
spiel betrachtet. Hier ist nun zu erkennen, dass
nicht nur der Trend der Kurve – wie bei den an-
deren beiden Methoden – sondern auch die
saisonalen Schwankungen erkannt werden. Die
ist wiederum auch ein Nachteil, denn dieser
Glättungsparameter kann nicht objektiv be-
stimmt werden. Darüber hinaus gibt es, abge-
sehen von der Zeit, keine weiteren Einflussfak-
toren. Muster innerhalb der Daten können auch
mit dieser Methode nicht erkannt werden (vgl.
Abbildung 3).
Vergleicht man die beiden Kurven, ist in diesem
Beispiel nur ein marginaler Unterschied zwi-
schen den beiden Methoden zu erkennen (vgl.
Abbildung 4).
Autoregressiver integrierter gleitender
Durchschnitt
Eine in der Reihe der statistischen Zeitreihenana-
lysen häufig genutzte Methode ist der „autore-
gressive integrierte gleitende Durchschnitt“ (engl.
Auto Regressive Integrated Moving Average, kurz
ARIMA). Im Laufe der Modellierung werden die
sogenannten „Ordnungen“ p, d und q des ARIMA
(p, d, q) Modells optimiert. Der autoregressive Teil
(AR) beschreibt hierbei die lineare Abhängigkeit
der Zielvariable von seinen p-gewichteten Ver-
gangenheitswerten. Moving Averages (MA) sind
gleitende Durchschnittsprozesse q-ter Ordnung.
Das d bestimmt die Anzahl benötigter Differenzie-
rungen, um eine stationäre Zeitreihe zu erhalten,
die keine systematischen Abweichungen auf-
weist. Durch die Differenzierung(en) werden vor-
handene Abweichungen zum Mittelwert elimi-
niert. Ist eine Zeitreihe nicht stationär, so nennt
man diese „integriert“. Mithilfe eines ARIMA-Mo-
dells können kurzfristige Prognosen in die Zu-
kunft vorgenommen werden.
Abb. 4: SMA vs. ES
Abb. 5: AMIRA vs. IST
CM November / Dezember 2018
Abb. 6: Fehlergrenzen Umsatzbeispiel


